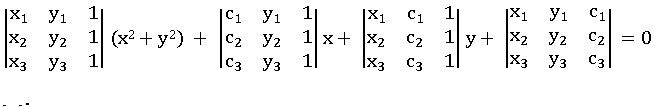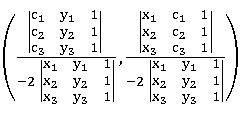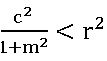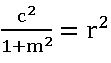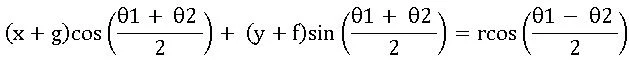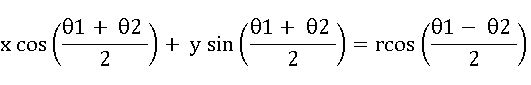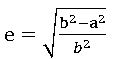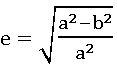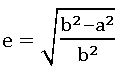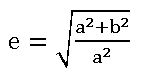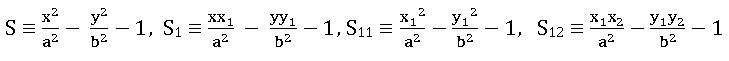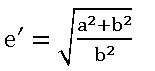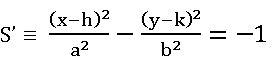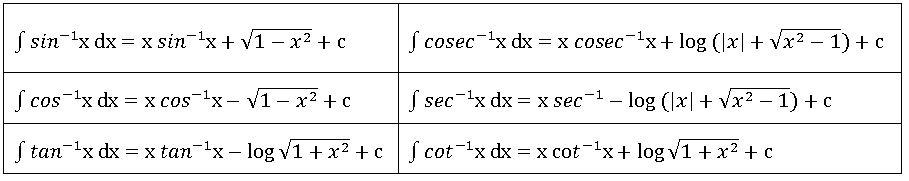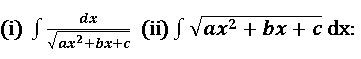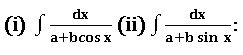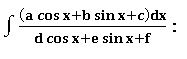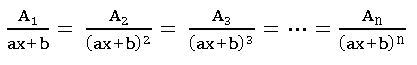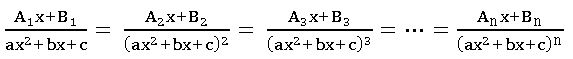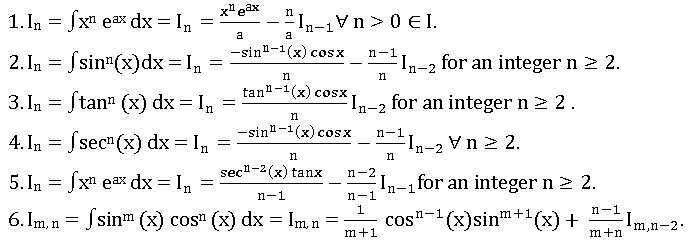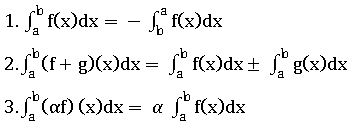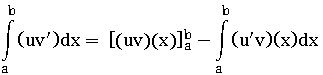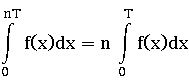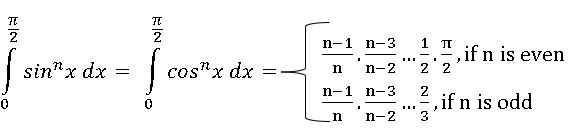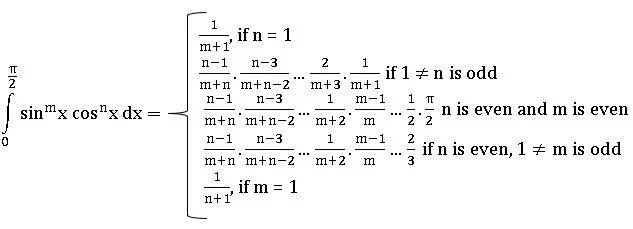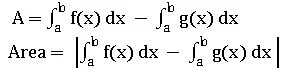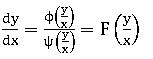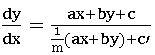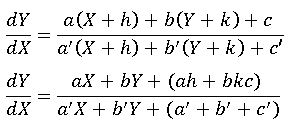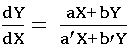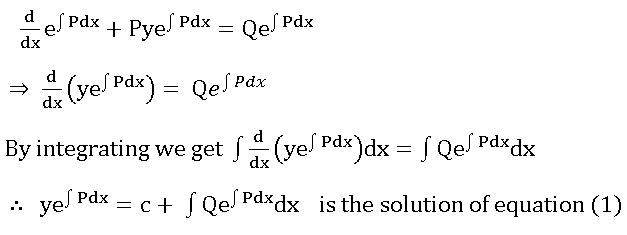TS Inter second year
TS Inter second year: This note is designed by the ‘Basics in Maths’ team. These notes to do help the TS intermediate second-year Maths students fall in love with mathematics and overcome the fear.
These notes cover all the topics covered in the TS I.P.E second year maths 2B syllabus and include plenty of formulae and concept to help you solve all the types of Inter Math problems asked in the I.P.E and entrance examinations.
TS Inter second year
1. CIRCLES
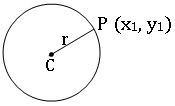
Circle: In a plane, the set of points that are at a constant distance from a fixed point is called a circle.
∗ The fixed point is called the centre (C) of the circle and the constant distance is called the radius(r) of the circle
Unit circle: If the radius of the circle is 1 unit, then that circle is called the unit circle.
Point Circle: A circle is said to be a point circle if its radius is zero. A point circle contains only one point in the centre of the circle. •
∗ The equation of the circle with centre (h, k) and radius r is 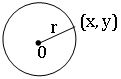
(x – h)2 + (y – k)2 = r2
∗ The equation of the circle with centre origin and radius r is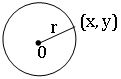
x2 + y2 = r2
⇒ x2 + y2 = r2 is called standard form of the circle.
The general equation of the second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, where a, b, f, g, h and c are real numbers, represent a circle iff (i) a = b ≠ 0 (ii) h = 0 and (iii) g2 + f2 + c ≥ 0
∗ The general equation of the circle is x2 + y2 + 2gx + 2fy + c = 0
It’s centre c = (– g, – f) and radius ![]()
∗ The equation of the circle passing through origin is x2 + y2 + 2gx + 2fy = 0.
∗ The equation of the circle whose centre on the x-axis is x2 + y2 + 2gx + c = 0.
∗ The equation of the circle having centre on y-axis is x2 + y2 + 2fy + c = 0.
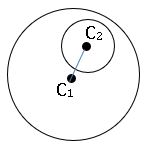
∗ The circles which have the same centre are called concentric circles.
∗ The equation of the circle concentric with the circle x2 + y2 + 2gx + 2fy + c = 0 is
x2 + y2 + 2gx + 2fy + k = 0.
∗ The length of the intercept made by a circle x2 + y2 + 2gx + 2fy + c = 0 on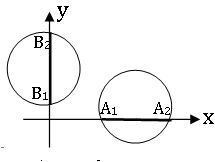
Note: –
(a) if g2 – c = 0, then A1 A2 = 0 ⇒ the circle touches the x- axis at only one point.
(b) if f2 – c = 0, then B1 B2 = 0 ⇒ the circle touches the y- axis at only one point.
(c) if g2 – c < 0, then the circle does not meet the x- axis.
(d) if f2 – c < 0, then the circle does not meet the y- axis.
∗ The equation of the circle having the line segment joining A (x1, y1) and B (x2, y2) as a diameter is
(x – x1) (x – x2) + (y – y1) (y – y2) = 0.
∗ Let A, B be any two points on a circle then,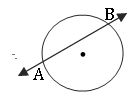
- The line is called the secant line of the circle.
- The line segment is called the chard of the circle.
- AB is called the length of the chord.
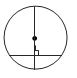
∗ A chord passing through the centre is called the diameter of the circle.
∗ The angle subtended by a chord on the circumference of at any point is equal.
The perpendicular bisector of a chord of a circle is asses through the centre of the circle.
∗ The angle in a semicircle is 900.
∗ The equation of the circle passing through three non-collinear points A (x1, y1), B (x2, y2), C (x3, y3) is
Where ci = − (x2 + y2) and i = 1,2,3
∗ centre of the circle is
Parametric form:
If P (x, y) is a point on the circle with centre (h, k) and radius r, then
X = h + r cosθ, y = k + r sinθ 0 ≤ θ ≤ 2π.
⇒ A point n the circle x2 + y2 = r2 is taken as (r cosθ, r sinθ) and simply denoted by θ.
Note:
- If the centre of the circle is the origin, then the parametric equations are x = r cosθ, y = r, 0 ≤ θ ≤ 2π.
- The point (h + rcosθ1, k + r sin θ1) is referred to as the point θ1 on the circle having the centre (h, k) and radius r.
Notations:
S = x2 + y2 + 2gx + 2fy + c
S1 = xx1 + yy1 + g(x +x1) + f (y +y1) + c
S11 = x12 + y12 + 2gx1 +2fy1 + c
S12 = x1x2 + y1y2 + g(x1 + x2 ) + f (y1 + y2) + c
Position of a point with respect to the circle: 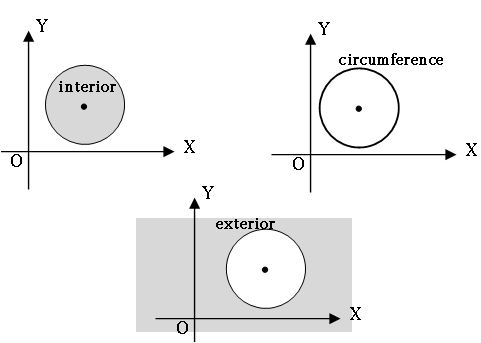
A circle divides the plane into three parts.
1. The interior of the circle
2. The circumference which is the circular curve.
3. The exterior of the circle.
Power of point:
Les S = 0 be a circle with radius ‘r’ and centre ‘C’ and P (x1, y1) be a point on the circle, then CP – r2 is called the power of point ‘P’ concerning S = 0.
- The power of point P (x1, y1) w.r.t. S = 0 is S11.
•Let S = 0 be a circle in a plane and P (x1, y1) be any point in the same plane. then
- P lies in the interior of the circle ⇔ S11 < 0.
- P lies on the circle ⇔ S11 = 0.
- Plies in the exterior of the circle ⇔ S11 > 0.
Secant and tangent of a circle:
Let P be any point on the circle and Q be neighbourhood point of P lying on the circle. join P and Q, then the line PQ is the secant line.
The limiting position of the secant line PQ when Q is approached to the point P along the circle is called a tangent to the circle at P.
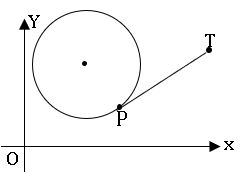
If P is any point on the circle S = 0 and T is any exterior point of the circle, then PT is called the length of the tangent.
∗ If S = 0 is a circle and P (x1, y1) is an exterior point with respect o S = 0, then the length of the tangent from P (x1, y1) to S =0 is ![]()
Condition for a line to be a tangent:
- A straight-line y = mx + c (i) meet the circle x2 + y 2 = r2 in two distinct points if

- Touch the circle x2 + y 2 = r2 if

- Does not touch the circle x2 + y 2 = r2 in two distinct points if

Note:
- For all real values of m, the straight line
 is a tangent to the circle x2 + y2 = r2 and the slope of the line is m.
is a tangent to the circle x2 + y2 = r2 and the slope of the line is m. - A straight-line y = mx + c is a tangent to the circle x2 + y2 = r2 if c =
 .
. - The equation of a tangent to the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 having the slope m is
 where r is the radius of the circle.
where r is the radius of the circle. - The circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 touches (i) x – axis if g2 = c (ii) y – axis if f2= c.
Chord joining two points on a circle:
If P (x1, y1) and Q (x2, y2) are two points on the circle S = 0 then the equation of secant line PQ is S1 + S2 = S12.
Equation of tangent at a point on the circle:
The equation of the tangent at the point (x1, y1) to the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 is S1 = 0.
The equation of the tangent at the point (x1, y1) to the circle x2 + y2 = r2 is xx1 + yy1 – r2 = 0.
Point of contact:
If a straight-line lx + my + n = 0 touches the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 at P (x1, y1), then this line is the tangent to the circle S = 0. And the equation of the tangent is
(x1 + g) x + (y1 +f) y + (gx1 + fy1 + c) = 0.
∗ The equation of the chord joining two points θ1, θ2 on the circle x2 + y2 + 2gx + 2fy + c = 0 is
∗ The equation of the chord joining the points θ1, θ2 on the circle x2 + y2 = r2 is
∗ The equation of the tangent at P(θ) on the circle x2 + y2 + 2gx + 2fy + c = 0 is
∗ The equation of the tangent at P(θ) on the circle x2 + y2 = r2 is
x cosθ + y sinθ = r.
The normal at any point P of the circle is the line which is passing through P and is perpendicular to the tangent at P.
- The equation of the normal at P (x1, y1) of the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 is
(x – x1) (y1 + g) – (y – y1) (x1 + g) = 0.
- The equation of the normal at P (x1, y1) of the circle x2 + y 2 = r2 is xy1 – yx1 = 0.
Chord of contact and Polar:
∗ If P (x1, y1) is an external point of the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0, then there exists two tangents from P to the circle S = 0.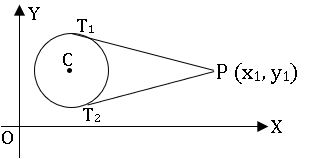
Chord of contact: –
If the tangents are drawn through P (x1, y1)
to a circle S = 0 touch the circle at points A and B then the secant line AB is called the chord of contact of P with respect to S = 0
∗ If P (x1, y1) is an external point of the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0, then the equation of the chord of contact of P with respect to S =0 is S1 = 0.
Note:
- If the point P (x1, y1) is on the circle S = 0, then the tangent itself can be defined as the chord of contact.
- If the point P (x1, y1) s an interior point of the circle S = 0, then the chord of contact does not exist.
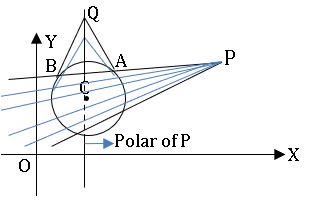
Let S = 0 be a circle and P be any point if any line is drawn through the point Pin the plane other than the centre of S = 0. then the points of intersection meet the circle in two points A and B, of tangents drawn at A and B lie on a line called polar of P and P, is called Pole of polar.
∗ The equation of the polar of P (x1, y1) with respect to the circle S = 0 is S1 = 0.
Note: –
- If Plies outside the circle S = 0, then the polar of P meets the circle in two points and the polar becomes the chord f contact of P.
- If P lies on the circle S = 0, then the polar P becomes the tangent at P o the circle.
- If P lies inside the circle S = 0, then the polar of P does not meet the circle.
- If P is the centre of the circle S = 0, then the polar of P does not exist.
- The pole of the line lx + my + n = 0 with respect to the circle x2 + y2 = r2 is
- The pole of the line lx + my + n = 0 with respect to the circle x2 + y2 + 2gx + 2fy + c = 0 is
- The polar of P (x1, y1) with respect to the circle S = 0 passes through Q (x2, y2) ⟺ polar of Q passes through P.
Conjugate points: Two P and Q are said to be conjugate points with respect to the circle S = 0, if the polar of P with respect to S = 0 passes through Q.
⇒ The condition for the points P (x1, y1), Q (x2, y2) to be conjugate with respect to the circle S = 0 is S12 = 0.
Conjugate lines: Two lines L1 = 0 and L2 = 0 are said to conjugate lines with respect to the circle S = 0 if the pole of L1 = 0 is lies on L2 = 0.
⇒ The condition for the lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate with respect to the circle S ≡ x2 + y2 + 2gx + 2fy + c = 0 is
r2 (l1l2 + m1m2) = (l1g + m1f – n1) (l2g + m2f – n2)
⟹ The condition for the lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate with respect to the circle S ≡ x2 + y2 = r2 is r2 (l1l2 + m1m2) = n1n2
Inverse points: Let S = 0 be a circle with centre C and radius r. two points P and Q are said to be inverse points with respect to the circle S = 0 if
- C, P, Q are collinear.
- P, Q lies on the same side of C.
- CQ = r2.
⟹ If lies inside of the circle S = 0, then Q lies outside of the circle.
⟹ If P lies on the circle S = 0, then P =Q.
⟹ Let S = 0 be a circle with centre C and radius r. The polar of P meets the line CP in Q iff P, Q is inverse points.
⟹ f P, Q are inverse points with respect to S = 0, then P, Q are conjugate points with respect to the circle S = 0.
⟹ If P, Q are inverse points with respect to S = 0, then Q is the foot of the perpendicular from P on the polar of P with respect to the circle S = 0.
Equation of the chord with the given middle point:
The equation of the chord of the circle S = 0 having P (x1, y1) as its midpoint is S1 = S11.
Common tangents to the circle: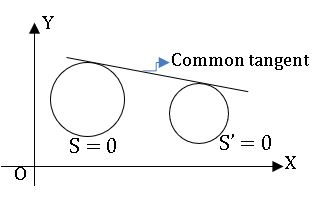
⟹ A straight line L = 0 is said to be a common tangent to the circle S = 0 and S’= 0 if it is a tangent to both S = 0 and S’ = 0.
⟹ Two circles are said to touch each other if they have only one common tangent.
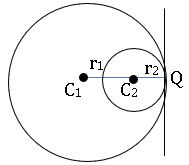
The relative position of two circles:
Let C1, C2 centres and r1, r2 be the radii of two circles S = 0 and S’ = 0respectively.
1.If C1C2 > r1+ r2, then two circles do not intersect.
⟹2 direct common tangents and
2 transverse common tangents
Total 4 common tangents
⟹P divides C1C2 in the ratio r1: r2 internally
Here P is called the internal centre of similitude (I.C.S)
⟹ Q divides C1C2 in the ratio r1: r2 externally
Here Q is called the external centre of similitude (E.C.S)
2.If C1C2 = r1+ r2, two circles touch each other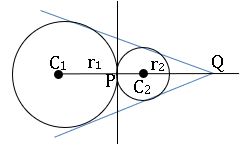
⟹ Q divides C1C2 in the ratio r1: r2 externally
⟹ two direct common tangents and one common tangent. Total 3 tangents
Here Q is called the external centre of similitude (E.C.S)
Here Q is called the external centre of similitude (E.C.S)
⟹ Q divides C1C2 in the ratio r1: r2 externally
⟹ internal centre of similitude does not exist.
⟹ only one common tangent
⟹ internal centre of similitude does not exist.
⟹ no. of common tangents zero.
Note: the combined equation of the pair of tangents drawn from an external point P (x1, y1) to the circle S = 0 is S S11 = S12.
2.SYSTEM OF CIRCLES
A set of circles is said to be a system of circles if it contains at least two circles.
The angle between two intersecting circles:
⟹ If two circles S = 0 and S’ = 0 intersect at P then the angle between the tangents of two circles at P is called angle between the circles at P.
⟹ If two circles S = 0 and S’ = 0 intersect at P and Q then the angle between the tangents of two circles at P and Q are equal.
⟹ If d is the distance between the centres of the two intersecting circles with radii r1, r2 and θ is the angle between the circles then.
⟹ If θ is the angle between the circles x2 + y2 + 2gx + 2fy + c = 0 and x2 + y2 + 2g’x + 2f’y + c’ = 0 then
⟹ Two intersecting lines are said to be Orthogonal if the angle between the circles is a right angle.
Condition for the orthogonality:
⟹ The condition that the two circles x2 + y2 + 2gx + 2fy + c = 0 and x2 + y2 + 2g’x + 2f’y + c’ = 0 cut each other orthogonally is 2gg’ + 2ff’ = c + c’.
⟹ If d is the distance between the centres of the two intersecting circles with radii r1, r2. Two circles cut orthogonally if d2 = r12 + r22.
∎ If S = 0, S’ = 0 are two circles intersecting at two distinct points, then S – S’ = 0 represents a common chord of these two circles.
∎ If S = 0, S’ = 0 are two circles touch each other, then S – S’ = 0 represents a common tangent of these two circles.
∎ If S ≡ x2 + y2 + 2gx + 2fy + c = 0 and L ≡ lx + my + n = 0 are the equation of the circle and a line respectively intersecting each other, then S + λ L = 0 represent a circle passing through the point intersection of S = 0 and L = 0 ∀ λ ∈ ℛ.
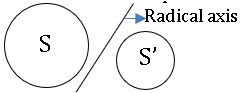
The radical axis of two circles s defined as the locus of the point which moves so that its powers with respect to the two circles are equal.
(OR)
The locus of a point, for which the powers with respect to given non-concentric circles are equal, is a straight line is called Radical axis of the given circles.
∎ The equation of Radical axis f the circles S = 0 and S’ = 0 is S – S’ = 0.
→ The radical axis of any two circles is perpendicular to the line joining their centres.
→ The lengths of tangents from a point on the radical axis of two circles are equal if exist.
→ Radical axis of two circles bisects all common tangents of the two circles.
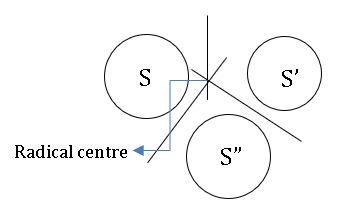
∎ If the centres of any three circles are non-collinear then the radical axis of each pair of circles chosen from these three circles re concurrent.
Radical centre: The point of concurrence of radical axes of each pair of three circles is called radical centre (see above figure).
∎ If the circle S = 0 cuts the each of the two circle S’ = 0 and S’’ =0 orthogonally then the centre of S =0 lies on the radical axis of S’ = 0 and S’’ = 0.
∎ Radical axis of two circles is
- The ’common chord’ if the two circles intersect at two distinct points.
- The ‘common tangent’ at the point of contact if the two circles touch each other.
→ The radical axis of any two circles bisects the line joining the points of contact of common tangents to the circles.
→ Let S = 0, S’ = 0 and S’’ =0 be three circles whose centres are non- collinear and no two circles of these are intersecting then the circles having
- Radical centre of these circles as the centre of the circle.
- Length of the tangent from the radical centre to any one of these three circles cuts the given three circles orthogonally.
CONIC SECTIONS
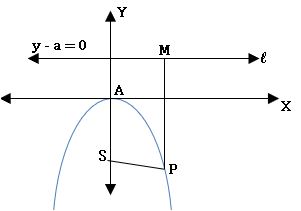
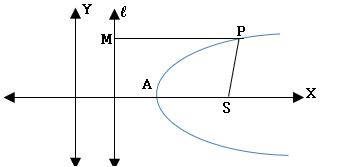
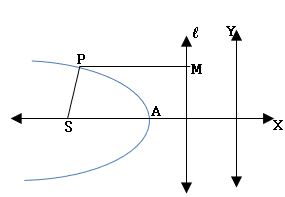
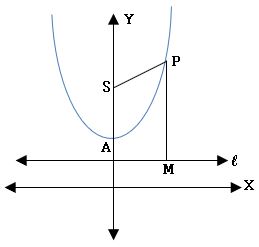
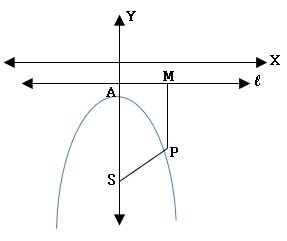
Conic: The locus of a point moving on a plane such that its distance from a fixed point and a fixed straight line is in the constant ratio is called Conic.
OR
The locus of a point moving on a plane such that its distance from a fixed point and a fixed line on the plane are in a constant ratio ‘e’, is called a Conic.
Focus: The fixed point is called focus and it is denoted by S.
Directrix: The fixed straight line is called the directrix.
Eccentricity: The constant ratio is called eccentricity and it is denoted by ‘e’.
⟹ Conic is the locus of a point P moving on a plane such that SP/PM = e, PM is the perpendicular distance from P to directrix at M.
⟹ If e = 1, then the conic is parabola.
⟹ if 0 < e < 1, then the conic is Ellipse.
⟹ if e > 1, then the conic is Hyperbola.
3.PARABOLA
If e = 1, then the conic is parabola.
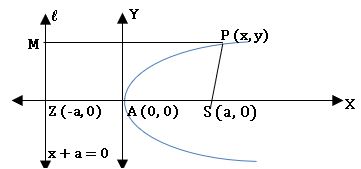
- The standard form of parabola is y2 = 4ax.
- Focus S = (a. 0).
- Equation of directrix is x + a = 0.
- Vertex A = (0, 0) and A is the mid-point of SZ.
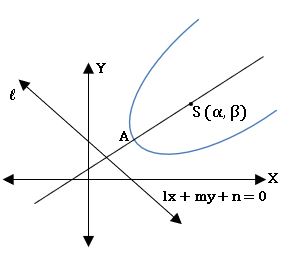
• Equation of the parabola with focus (α, β) and directrix lx + my + n = 0 is
- If the focus is situated on the left side of the directrix, the equation of the parabola with vertex as the origin and the axis is X-axis is y2 = – 4ax.
- The vertex being the origin, if the axis of the parabola is taken as Y – axis, equation of the parabola is x2 = 4 ay or x2 = – 4 ay according to the focus is above or below the X-axis.
Nature of the curve:
The nature of the parabola f the equation y2 = 4 ax (a>0)
- F y = 0, then 4 ax = 0 and x = 0
∴ the curve passes through the origin.
- If x = 0, then y2 = 0. Which gives y = 0. Y – axis is the tangent to the parabola at origin.
- Let P(x, y) be any point on the parabola (a>0) and y2 = 4 ax, we have x ≥ 0 and

∴ for any positive real value of x, we obtain two value of y of equal magnitude but opposite in sign. This shows that the curve is symmetric about X-axis and lies in the first and fourth quadrants.
The curve does not exist on the left side of the Y-axis since x ≥ 0 for any point (x, y) on the parabola.
Chord: The line segment joining two points on a parabola is called a chord.
Focal chord: A chord which is passing through focus is called Focal Chord.
Double ordinate: A chord through a point P on the parabola, which is perpendicular to the axis of the parabola is called Double ordinate.
Latus rectum: The double ordinate passing through the focus is called Latus rectum.
⟹ Length of Latus rectum = 4a.
Various forms of the parabola
focus: (a, 0)
equation of directrix: x + a = 0
axis of parabola: y = 0
vertex: (0. 0)
equation of directrix: x − a = 0
focus: (−a, 0)
axis of parabola: y = 0
vertex: (0. 0)
focus: (0, a)
equation of directrix: y + a = 0
axis of parabola: x = 0
vertex: (0. 0)
focus: (0, −a)
equation of directrix: y − a = 0
vertex: (0. 0) axis of parabola: x = 0
focus: (h + a, k)
equation of directrix: x – h + a = 0
axis of parabola: y – k = 0
vertex: (h. k)
focus: (h – a, k)
equation of directrix: x – h – a = 0
axis of parabola: y – k = 0
vertex: (h. k)
focus: (h, k + a)
equation of directrix: y – k + a = 0
axis of parabola: x – h = 0
vertex: (h. k)
focus: (h, k – a)
equation of directrix: y – k – a = 0
vertex: (h. k)
axis of parabola: x – h =0
focus: (α, β)
equation of directrix: lx + my + n = 0
axis of parabola: m (x – α) – l (y – β) = 0
vertex: A
Note:
- Equation of the parabola whose axis parallel to X – axis is x = ly2 + my + n.
- Equation of the parabola whose axis parallel to Y – axis is y = lx2 + mx + n.
Focal distance: The distance of a point on the parabola from its focus is called Focal distance.
⟹ Focal distance of parabola s x1 + a
Parametric equations of a parabola:
The point (at2, 2at) satisfy the equation y2 = 4ax, the parametric equations of parabola are x = at2, y = 2at. The point P(at2, 2at) is generally denoted by the point ‘t’ or P(t).
Notation:
- S ≡ y2 – 4 ax
- S1 ≡yy1 – 2a (x + x1)
- S12 ≡ y1y2 – 2a (x1 + x2)
- S11 ≡ y12 – 4 ax1
Equation of a tangent and normal at a point on the parabola:
∎ y = mx + c is a tangent to the parabola y2 = 4ax, then c = a/m or a =cm, and the point of contact is (a/m2, 2a/m).
∎ if m = 0, the line y = c is parallel to the axis of the parabola (i.e., x – axis)
y = c ⟹ c2 = 4ax ⟹ x = c2 /4a
∴ point of contact is (c2/4a, c).
∎ if m ≠ 0 and c = 0, then
Y = mx ⟹ x = 4a/m2 and y = 4a/m
∴ point of contact is (4a/m2, 4a/m).
∎ The equation of the chord joining the points (x1, y1) and (x2, y2) is S1 + S2 = S12.
∎ The equation of the tangent at P (x1, y1) to the parabola S = 0 is S1= 0.
∎ The equation of the normal at P (x1, y1) is (y – y1) = – y1/2a (x – x1).
Parametric form:
∎ The equation of the tangent at a point ‘t’ on the parabola y2 = 4ax is x – yt + at2 = 0.
∎ Equation of the normal at a point ‘t’ on the parabola y2 = 4ax is y + xt = 2at + at3.
∎ The condition for the straight-line lx + my + n = 0 to be a tangent to the parabola y2 = 4 ax is
am2 = nl and point of contact is (n/l, –2 am/l).
∎ common tangent to the parabolas y2 = 4 ax and x2 = 4 by is x a1/3 + y b1/3 + a2/3 b2/3 = 0.
∎ The equation of the chord of contact of the external point (x1, y1) w.r. t parabola S = 0 is S1 = 0.
∎ The equation of the polar of the point (x1, y1) w.r. t parabola S = 0 is S1 = 0.
∎ The pole of the line lx + my + n = 0 w.r.t. parabola y2 = 4ax is (n/l, -2am/l).
∎ If two points P (x1, y1), Q (x2, y2) are conjugate points w.r.t. parabola S = 0, then S12 = 0.
∎ The lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 are conjugate lines with respect to the parabola y2 = 4 ax, then l1n2 + l2n1 = 2a m1m2.
4.ELLIPSE
Ellipse: A conic with eccentricity less than unity s called Ellipse.
∎ Equation of Ellipse in standard form is ![]()
⇒b2 = a2 (1 – e2) ⇒ e2 – 1 = -b2/a2
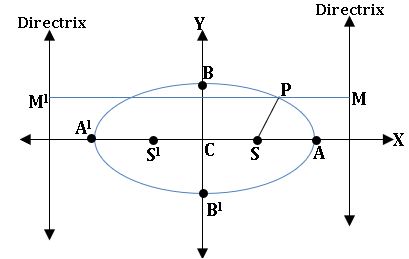
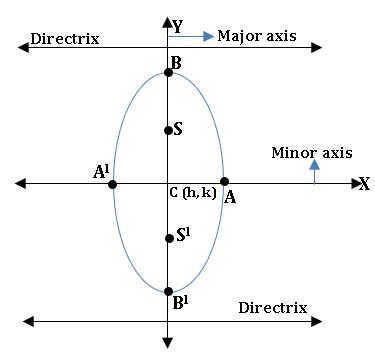
Major and Minor axis:
⟹ The line segment AA’ and BB’ of length 2a and 2b respectively are axes of the Ellipse.
⟹ If a > b AA’ is called Major axis and BB’ is called Minor axis and vice-versa if a<b.
Various form of Ellipse:
Major axis: along the x-axis
Length of Major axis:2a
Minor axis: along y – axis
Length of Minor Axis:2b
Centre: (0, 0)
Foci: S = (ae, 0) and S’ = (–ae, 0)
Equation of directrices: x = a/e and x = –a/e
Major axis: along y – axis
Length of Major axis:2b
Minor axis: along x – axis
Length of Minor Axis:2a
Centre: (0, 0)
Foci: S = (0, be) and S’ = (0, –be)
Equation of directrices: x = b/e and x = –b/e
Centre not at the origin
Major axis: along with y = k
Length of Major axis:2a
Minor axis: along x = h
Length of Minor Axis:2b
Centre: (h, k)
Foci: S = (h +ae, k) and S’ = (h – ae, k)
Equation of directrices: x = h + a/e and x = h – a/e
Major axis: along x = h
Length of Major axis:2b
Minor axis: along with y = k
Length of Minor Axis:2a
Centre: (h, k)
Foci: S = (h, k + be) and S’ = (h, k – be)
Equation of directrices: xy = k + b/e and y = k – b/e
Chord: The line segment joining two points on a parabola is called a chord of Ellipse.
Focal chord: A chord which is passing through one of the foci is called Focal Chord.
Latus rectum: A focal chord perpendicular to the major axis of the Ellipse is called Latus Rectum. Ellipse has two latera recta.
Length of the Latus rectum:
1.The coordinates of the four ends of the latera recta of the ellipse ![]()
L = (ae, b2/a), L’ = (ae, -b2/a) and L1 = (-ae, b2/a), L1’= (-ae, -b2/a).
length of the Latus rectum = 2b2/a.
2.length of the Latus rectum of an ellipse ![]() is 2a2/b and the coordinates of the four ends of the latera recta are
is 2a2/b and the coordinates of the four ends of the latera recta are
L = (a2/b, be), L’ = (-a2/b, be) and L1 = (a2/b, -be), L1’ = (-a2/b, -be).
3. The equation of the Latus rectum of the Ellipse ![]() through S is x = ae and through S’ is x = -ae.
through S is x = ae and through S’ is x = -ae.
4. The equation of the Latus rectum of the Ellipse ![]() through S is y = be and through S’ is y = -be.
through S is y = be and through S’ is y = -be.
5. If P (x, y) is any point on the Ellipse ![]() whose foci are S and S’, then SP +S’P is constant.
whose foci are S and S’, then SP +S’P is constant.
Auxiliary circle: The circle described on the major axis of an Ellipse as the diameter is called the Auxiliary circle of the Ellipse. The Auxiliary circle of the Ellipse ![]() is x2 + y2 = a2.
is x2 + y2 = a2.
Parametric equations: The parametric equations of the Ellipse ![]() are x = a cosθ and y = b sinθ.
are x = a cosθ and y = b sinθ.
Notation:
Equation of Tangent and Normal
∎ The equation of any tangent to the Ellipse can be written as ![]()
∎ The condition for a straight-line y = mx + c to be a tangent to the Ellipse ![]() is c2 = am2 + b2.
is c2 = am2 + b2.
∎ The point of contact of two parallel tangents to the Ellipse are (-a2m/c, b2/c) and (a2m/c, -b2/c)
∎ The equation of the chord joining two points (x1, y1) and (x2, y2) on the Ellipse S = 0 is S1 + S2 = S12.
∎ The equation of the Normal at P (x1, y1) to the Ellipse is ![]()
∎ Equation of the tangent at P(θ) on the Ellipse ![]()
∎ Equation of the normal at P(θ) on the Ellipse S = 0 is![]()
∎ When θ = 0, π; equation of Normal is y =0.
∎ When θ = π/2, 3π/2; equation of Normal is x =0.
∎ The condition for the line lx + my + n = 0 to be a tangent the Ellipse S = 0 is a2l2 + b2m2 = n2.
∎ The condition for the line x cosα + y sinα = p to be a tangent the Ellipse S = 0 is a2 cos2 α + b2 sin2 α = p2.
∎ The pole of the line lx + my + n = 0 with respect to the Ellipse S = 0 is (-a2l/n, -b2m/n).
∎ The condition for the two lines l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0 to be conjugate with respect to the Ellipse S = 0 is a2l1l2 + b2m1m2 = n1n2. a2l1l2.
5.HYPERBOLA
Hyperbola: Hyperbola is a conic in which the eccentricity is greater than the unity.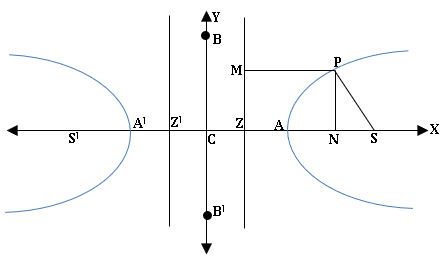
Standard form of Hyperbola:
Equation of Hyperbola in standard form is ![]()
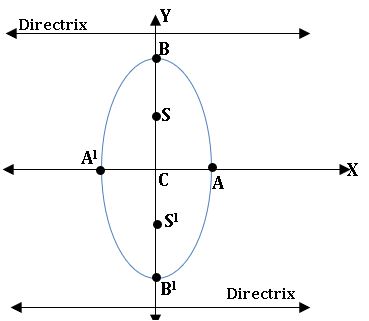
Centre: C (0, 0)
Foci: (± ae, 0)
Directrix: x = ± a/e.
Rectangular Hyperbola:
If in a Hyperbola the length of the transverse axis (2a) is equal to the length of the conjugate axis(2b), then the hyperbola is called rectangular hyperbola.
Its equation is x2 – y2 = a2 and eccentricity is ![]() .
.
Auxiliary circle: The circle described on the transverse axis of hyperbola as diameter is called the auxiliary circle of the hyperbola.
The equation of the auxiliary circle of S = 0 is x2 + y2 = a2.
Parametric equations: The parametric equations of the Parabola S = 0 are x = a secθ and y = b tanθ.
Conjugate Hyperbola:
The hyperbola whose transverse and conjugate axis are respectively the conjugate and transverse axis of a given hyperbola is called a conjugate hyperbola.
The equation of hyperbola conjugate to S ≡ is S’ ≡
The transverse axis lies on along X-axis and its length is 2a.
The conjugate axis lies on along Y-axis and its length is 2b.
∎ For ![]()
The transverse axis lies on along Y-axis and its length is 2b.
The conjugate axis lies on along X-axis and its length is 2a.
Let ![]() and
and ![]()
The transverse axis along X-axis: y =0
Length of the transverse axis:2a
The conjugate axis along Y-axis: x = 0
Length of the conjugate axis: 2b
Centre: (0, 0)
Foci: (± ae, 0)
Equation of the directrices: x = ± a/e
The transverse axis along Y-axis: x = 0
Length of the transverse axis:2b
The conjugate axis along X-axis: y = 0
Length of the conjugate axis: 2a
Centre: (0, 0)
Foci: (0, ± be)
Equation of the directrices: y = ± b/e
Centre not at the origin:
The transverse axis along X-axis: y = k
Length of the transverse axis:2a
The conjugate axis along Y-axis: x = h
Length of the conjugate axis:2b
Centre: (h, k)
Foci: (h± ae, k)
Equation of the directrices: x = h± a/e
The transverse axis along Y-axis: x = h
Length of the transverse axis:2b
The conjugate axis along X-axis: y = k
Length of the conjugate axis: 2a
Centre: (h, k)
Foci: (h, k ± be)
Equation of the directrices: y = k± b/e
Equation of tangent and normal at a point on the Hyperbola:
∎ The equation of the tangent at P (x1, y1) to the hyperbola S = 0 is S1 = 0.
∎ The equation of the tangent at P(θ) on the hyperbola S = 0 is ![]()
∎ The equation of the Normal at P (x1, y1) to the hyperbola S = 0 is 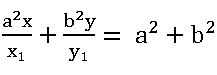
∎ Equation of the normal at P(θ) on the Hyperbola S = 0 is 
∎ The condition for a straight-line y = mx + c to be a tangent to the hyperbola S = 0 is c2 = am2 − b2.
Asymptotes of a hyperbola:
The equations of asymptotes of hyperbola S = 0 are ![]() and the joint equation of asymptotes is
and the joint equation of asymptotes is 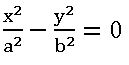
6. INTEGRATION
∎ Let E be a subset of R such that E contains a right or left the neighbourhood of each of its points and let f: E → R be a function. If there is a function F on E such that F’(x) = f(x) ∀ x ∈ E, then we call F an anti-derivative of f or a primitive of f.
Indefinite integral: Let f: I→R. Suppose that f has an antiderivative F on I. Then we say that f has an integral on I and for any real constant c, we call F + c an indefinite integral of over I, denote it by ∫f(x) dx and read it as ‘integral’ f(x) dx.
∫f = ∫f(x) dx = F(x) + c. here c is called constant of integration.
In the indefinite integral ∫f(x)dx, f is called ‘integrand’ and x is called the variable of integration.
⟹ if f: I⟶R is differentiable on I, then ∫f’(x)dx = f(x) + c.
Standard forms:
Properties of integrals:
∎ ∫ (f ±g) (x) dx = ∫f(x) dx ± ∫g(x) dx + c
∎ ∫(af) (x) dx = a ∫f(x) dx + c
∎ ∫ (f1 + f2 + … + fn) (x) dx = ∫f1(x) dx + ∫f2(x) dx + … +∫fn(x) dx +c
∎ ∫f(g(x)) g’(x) dx = F(g(x)) + c
∎ ∫f(ax + b) dx = 1/a F(ax +b) + c
Some important formulae:
- ∫eax dx = 1/a eax + c
- ∫sin (ax + b) dx = -1/a cos (ax + b) + c
- ∫cos (ax + b) dx = 1/a sin (ax + b) + c
- ∫sec2 (ax + b) dx = 1/a tan (ax + b) + c
- ∫ cosec2 (ax + b) dx = 1/a cot (ax + b) + c
- ∫cosec (ax + b) cot (ax + b) dx = -1/a cosec (ax + b) + c
- ∫sec (ax + b) tan (ax + b) dx = 1/a sec (ax + b) + c
Integration by parts:
Let u, v real valued differentiable functions in I. Suppose that u,v has an integral on I, then uv’ has an integral on I and
∫(uv’) (x) dx = (uv) – ∫(u’v) (x) dx + c or ∫(uv) dx = u ∫v dx – ∫ [u’ ∫v dx] dx + c
Integration of exponential functions:
∫ex dx = ex + c; ∫x ex dx = (x – 1) ex + c
∫ ex [f(x) +f’(x)] dx = ex f(x) + c
Integration of logarithmic functions:
∫log x dx = x log x – x + c
Integration of inverse trigonometric functions:
Evaluation of integrals form : ![]()
Working rule: reduce ax2 + bx + c to the form of a[(x + α)2 + β] and then integrate using the substitution t = x + α.
Working rule:
Case(i) if a >0 and b2 – 4ac < 0, then reduce ax2 + bx + c to the form of a[(x + α)2 + β] and then integrate.
Case(ii) if a <0 and b2 – 4ac >0, then reduce ax2 + bx + c to the form of (-a) [ β – (x + α)2 +] and then integrate.
Working rule: write px + q in the form of A (ax2 + bx +c)’ + B, then integrate.
Working rule: write cos x =cos2(x/2) – sin2(x/2) and sin x = 2 sin(x/2) cos (x/2)
Put t = tan(x/2), then dt = ½ sec2 (x/2) dx
Cos x = 1 – t2 / 1 + t2, sin x = 2t/1 + t2 then integrate.
Working rule: t = sqrt. (px + q and then integrate.
Working rule: we find real numbers A, B and C such that
(a cos x + b sin x + c) = A(d cos x + e sin x +f)’ + B(d cos x + e sin x +f) + C then by substituting this expression in the integrand, evaluate the integral.
Integration – partial fraction method:
Let R(x) = f(x) / g(x), g(x) ≠ 0 where f, g are polynomials. If degree of f(x) ≥degree of g(x), then divide f(x) by g(x) by synthetic division method and find polynomials.
Q(x) and h(x) such that f(x) = Q (x) g(x) + h(x) here h = 0 or h ≠ 0 and degree h(x) < degree of g(x). Then R(x) =Q(x) + h(x)/g(x)
We get solution of h(x) / g(x) using partial fractions and then integrate.
Partial fractions:
∎ If R(x) = f(x) / g(x) is proper fraction, then
Case(i): – For every factor of g(x) of the form (ax + b) n, there will be a sum of n partial fractions of the form:
Case(ii): – For every factor of g(x) of the form (ax2 + bx + c) n, there will be a sum of n partial fractions of the form:
∎ If R(x) = f(x) / g(x) is improper fraction, then
Case (i): – If degree f(x) = degree of g(x), then f(x)/g(x) = k + h(x)/g(x) where k is the quotient of the highest degree term of f(x) and g(x).
Case (ii): – If f(x) > g(x)
R(x) =f(x) /g(x) = Q(x) + h(x)/g(x)
Reduction formulas:
7.DEFINITE INTEGRATION
Partition: Let a, b∈ R be such that a < b. Then, a finite set P = {x0, x1, …, x i- 1, xi, xi + 1, …, xn} of elements of [a, b] is called to be a partition of [a, b] if a = x0 < x1 < … < x i- 1 < xi < xi + 1 < … < xn = b.
Norm: if {x0, x1, …, xn} is a partition of [a, b], then the norm of the partition P, denoted by ∥P∥, is defined by ∥P∥ = max {x1 – x0, x2 – x1, …, xn – xn-1}. We donate the set of all partitions of [a, b] by 𝒫 ([a, b]).
Definite integral:
Riemann sum: Let f: [a, b] → R be a bounded function for all x in [a, b]. Let P = {x0, x1, …, x i- 1, xi, xi + 1, …, xn} be partition of [a, b], and t ∈ [xi-1, xi], for I = 1, 2, …, n. A sum of the form  is called Riemann sum of f relative to P.
is called Riemann sum of f relative to P.
Let f is Riemann integrable on [a, b]. if there exists a real number A such that S (P, f) approaches A as ∥P∥ approaches to ‘0’. In other words, given ϵ > 0, there is a δ > 0 such that ![]() for any partition P of [a, b] with ∥P∥ < δ irrespective of the choice of ti in [xi-1, xi]. Such an A, if exists, is unique and is denoted by
for any partition P of [a, b] with ∥P∥ < δ irrespective of the choice of ti in [xi-1, xi]. Such an A, if exists, is unique and is denoted by ![]() , it is read as the definite integral of f from a to b. an a is called the lower limit and b is called the upper limit. The function f in
, it is read as the definite integral of f from a to b. an a is called the lower limit and b is called the upper limit. The function f in![]() is called ‘integrand’.
is called ‘integrand’.
∎ if f: [a, b] → R is continuous, then is exists.
∎ If f is continuous on [0, p] where p is a positive integer then ![]()
The fundamental theorem of integral calculus:
If f is integrable on [a, b] and if there is a differentiable function F on [a, b] such that F’ = f, then ![]()
properties of definite integrals:
∎ Let f: [a, b] → R be bounded. Let c ∈ (a, b). then f is integrable on [a, b] if and only if it is integrable on [a, c] as well as on [c, b] and in this case
Method of substitution: Let g: [c, d] → R have continuous derivative on [c, d]. Let f: g([c, d]) → R be continuous. Then (fog) g’ is integrable on [c, d] and ![]()
∎ Let f be integrable on [a, b]. Then the function h, defined on [a, b] as h(x) = f (a + b – x)
∎ Let f be integrable on [0, a]. Then the function h, defined on [0, a] as h(x) = f (a – x)
∎ Let f: [-a, a] → R be integrable on [0, a]. Suppose that f is either odd or even. Then f is integrable on [-a, a] and 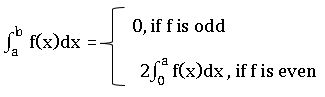
∎ Let f: [0,2 a] → R be integrable on [0, a].
- If f (2a – x) = f(x) for all x in [a, 2a] then f is integrable on [0, 2a] and

- If f (2a – x) = – f(x) for all x in [a, 2a] then f is integrable on [0, 2a] and

∎ If f and g are integrable on [a, b], then their product fig is integrable on [a, b].
Integration by parts:
∎ Let f: R→ R be a continuous periodic function and T be the period of it. Then any positive integer n
Reduction formulae:
∎ Let m and n be positive integers, then
Areas under curves:
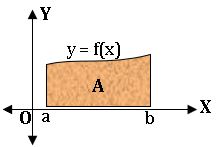
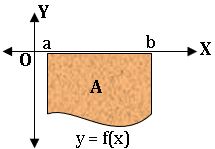
(i)If f: [a, b] → [0, ∞) is continuous, then the area A of the region bounded by the curve y = f(x), the X-axis and the line x = a and x =b is given by
(ii) If f: [a, b] → (−∞, 0] is continuous, then the graphs of y = f(x)and y = − f(x) on [a, b] are symmetric about the X-axis. So, the area bounded by the graph of y = f(x), the X-axis and the lines x = a, x =b is same as the area bounded by the graph of y = – f(x), the X-axis and the lines x = a and y = b which is given by A = ![]()
(iii) Let f: [a, b] → R be continuous and f(x) ≥ 0 ∀ x ∈ [a, c] and f(x) ≤ 0 ∀ x∈ [c, b] where a < c < b. Then the area of the region bounded by the curve y= f(x), the X – axis, and the lines x = a and x = b is given by ![]()
(iv) Let f: [a, b] → R and g: [a, b] → R be continuous f(x) ≤ g(x) ∀ x∈ [a, b]. Then the area f the region bounded by the curve y = f(x), y = g(x) and 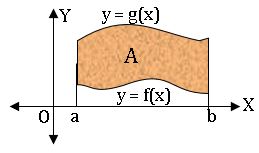 the lines x = a, x = b is given by
the lines x = a, x = b is given by
(v) Let f and g be wo continuous real value functions on [a, b] and c ∈ (a, b) such that f(x) < g(x) ∀ x∈ [a, c) and g(x) < f(x) ∀ x∈ (c, b] with f (c) = g  (c). area of the region bounded by y = f (x), y = g(x), and the lines x = a, x = b is given by
(c). area of the region bounded by y = f (x), y = g(x), and the lines x = a, x = b is given by 
(vi) Let f: [a, b] → R and g: [a, b] → R be continuous functions. Suppose that, there exist points x1, x2 ∈ (a, b) 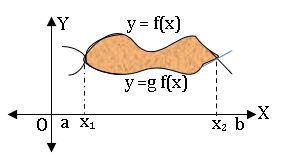 with x1< x2 such that f(x1) = g(x1) and f(x2) = g(x2) and f(x) ≥ g(x) ∀ x ∈ (x1, x2). Then the area of the region bounded by the curves by y = f (x), y = g(x), and the lines x = x1, x = x2 is given by
with x1< x2 such that f(x1) = g(x1) and f(x2) = g(x2) and f(x) ≥ g(x) ∀ x ∈ (x1, x2). Then the area of the region bounded by the curves by y = f (x), y = g(x), and the lines x = x1, x = x2 is given by![]() and if f(x) ≤ g(x) ∀ x ∈ (x1, x2). Then
and if f(x) ≤ g(x) ∀ x ∈ (x1, x2). Then![]() In either case, area is
In either case, area is 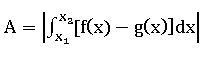 .
.
8. DIFFERENTIAL EQUATIONS
Differential equation: An equation involving one dependent variable and its derivative with respect to one or more independent variables is called a ‘Differential equation’.
If a differential equation contains only one independent variable, then it is called ‘an ordinary differential equation and if it contains more than one independent variable, then it is called ‘a partial differential equation’.
Degree of the differential equation: If a differential can be expressed as a polynomial equation in the derivatives occurring in it using the algebraic operations such that the exponent of each of the derivatives is the least, then the large exponent of the highest order derivative in the equation is called the degree of the differential equation.
Otherwise, the degree is not defined for a differential equation.
Order of differential equation: The order of the differential equation is the order of the highest derivative occurring in it.
Note: The general form of an ordinary differential equation of nth order is ![]()
Formation of the differential equation: suppose that an equation y = ϕ (x, α1, α2, …, αn) where α1, α2, …, αn are parameters, representing a family of curves is given. Then successively differentiating the above equation, a differential equation of the form ![]()
We know that y = mx is a straight line passing through the origin
Solving differential equations:
1. Variable separable method:
If a given differential equation can be put in the form of f(x) dx + g(y) dy = 0 then its solution can be obtained by integrating each of them. This method is called the variable separable method.
Ex: xdy – y dx = 0 can be written as dx/x =dy/y
By integrating we get ∫dx/x = ∫dy/y
⇒ logx = logy + logc
⇒ logx = log yc
∴ x = yc is the required solution
2. Homogeneous Differential Equation:
Homogeneous function: – A function f (x, y) of two variables x and y is said to be a homogeneous function of degree n, if f(kx, ky) = kn f(x, y) for all values of k for which both sides of the above are meaningful.
Homogeneous Differential Equation: – A differential equation of the form![]() where f (x, y) and g (x, y) are homogeneous functions of x and y of the same degree is called a homogeneous differential equation.
where f (x, y) and g (x, y) are homogeneous functions of x and y of the same degree is called a homogeneous differential equation.
Method of solving the homogeneous differential equation: –
Consider the homogeneous equation ![]() …… (1)
…… (1)
where f (x, y) and g (x, y) are homogeneous functions of x and y of the same degree.
f (x, y) = xn ϕ (y/x) and g(x) xn ψ (y/x)
from (2) and (3)
This can be solved by the variable separable method.
3. Non-Homogeneous Differential Equations:
The differential equation of the form![]() where a, b, c, a’, b’, c’ are constants and c and c’ are not both zero are called non-homogeneous equations. Reduce the above equation to a homogeneous equation by suitable substitution for x and y.
where a, b, c, a’, b’, c’ are constants and c and c’ are not both zero are called non-homogeneous equations. Reduce the above equation to a homogeneous equation by suitable substitution for x and y.
Case(i): –
Suppose that b = – a’. then ![]() becomes
becomes ![]()
⇒ (a’x + b’y + c’) dy – (ax – a’y + c) dx = 0
⇒ a’(x dy + y dx) + b’ y dy – ax dx + c’ dy – cdx = 0
By integrating we get
a’ xy + b’ y2/2 – a x2/2 + c’y – cx = k
which is a required solution.
Case(ii): –
Put ax + by = v, then
this can be solved by the variable separable method.
Case(iii): –
Suppose that b ≠ – a’ and a/a’ ≠ b/b’, then taking x = X + h, y = Y + k, where X and Y are variables and h, k are constants. We get ![]() . Hence
. Hence![]() …..(i) becomes
…..(i) becomes
Now choose constants h and k such that
ah + bk + c = 0
a’h + b’k +c’ = 0
by solving above equations, we get h. k values
This is the homogeneous equation in X and Y and then solve by the homogeneous method by putting Y = VX.
3. Linear Differential Equations:
A differential equation of the form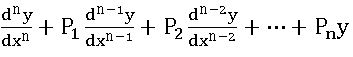 = R, where P1, P2, …, Pn and R are constants or functions x only, is said to be a linear differentiable equation of nth order.
= R, where P1, P2, …, Pn and R are constants or functions x only, is said to be a linear differentiable equation of nth order.
Method of solving the linear differentiable equation of 1st order: –
The linear differentiable equation of the first order is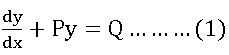
Multiplying both sides of (1) by![]() , we get
, we get
My App: Click Here
Visit my Youtube Channel: Click on Below Logo