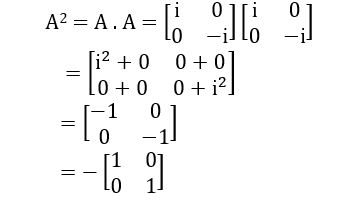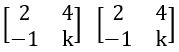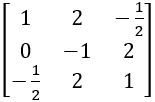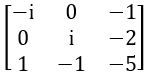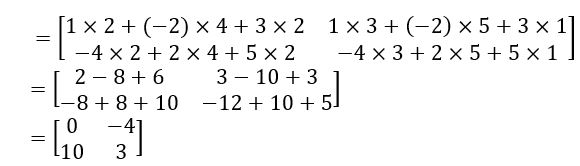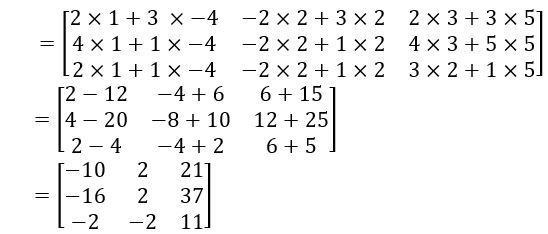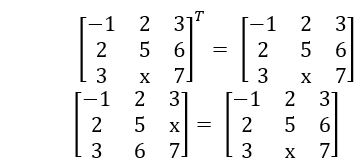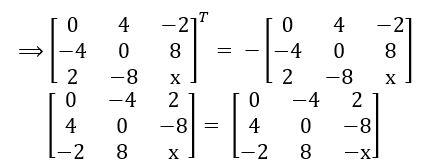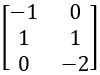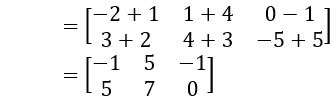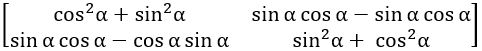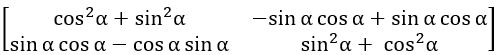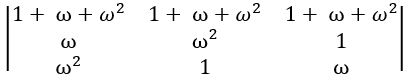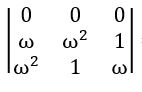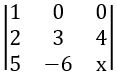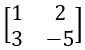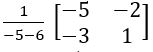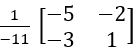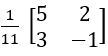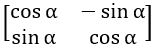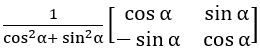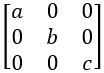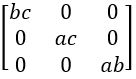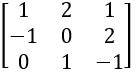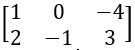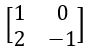Matrices ( Qns & Solutions) || V.S.A.Q’S||

Matrices ( Qns & Solutions) || V.S.A.Q’S||

Matrices V.S.A.Q’s: This note is designed by the ‘Basics in Maths’ team. These notes to do help intermediate First-year Maths students.

Inter Maths – 1A two marks questions and solutions are very useful in IPE examinations.

These notes cover all the topics covered in the intermediate First-year Maths syllabus and include plenty of solutions to help you solve all the major types of Math problems asked in the

IPE examinations.  

Matrices

QUESTION 1

If A = , then show that A² = –I

Sol: Given A =

  ∴  A² = –I

QUESTION 2

If A = , and A² = 0, then find the value of k.

Sol: Given A =  and

 A² = 0

⟹ A. A =0 ⟹     = 0

⟹  = 0

     8 + 4k = 0, – 2 – k = 0 and –4 + k² = 0

    4k = –8; k = –2; k² = 4

       k = –2; k = –2; k = ± 2

   ∴ k =– 2

QUESTION 3

Find the Trace of A, If A =

Sol: Given A =

       Trace of A = 1 – 1 + 1 = 1

QUESTION 4

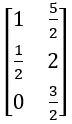
If A = , B = and 2X + A = B, then find X.

Sol: Given A = , B =  and 2X + A = B

        2X = B – A

        2X =  –

              =

              =

           X =  

         ∴ X =  

QUESTION 5

Find the additive inverse of A, If A =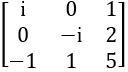

Sol: Given A =

       Additive inverse of A = – A

    = –

   =

QUESTION 6

If 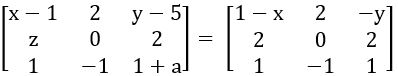, then find the values of x, y, z and a.

Sol: Given

 ⟹ x- 1 = 1 – x ; y – 5 =  – y ; z = 2 ; 1 + a = 1

 ⟹ x + x = 1 + 1; y + y = 5; z = 2; a =1– 1

  ⟹ 2x = 1; 2y = 5; z = 2; a = 0

∴ x = ½ ; y = 5/2; z = 2; a = 0

QUESTION 7

Construct 3 × 2 matrix whose elements are defined by a_ij =

Sol:

Let A=

a₁₁ =

a₁₁ = 1

a₁₂ =

a₁₂ =

a₂₁ =

a₂₁ =

a₂₂ =

a₂₂ = 2

a₃₁ =

a₃₁ = 0

a₃₂ =

a₃₂ =

 ∴ A =

QUESTION 8

If A = and B = 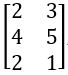, do AB and BA exist? If they exist, find them. BA and AB commutative with respect to multiplication.

Sol: Given Matrices are A =  B =

       Order of A = 2 × 3 and Order of B = 3 × 2

AB and BA exist

 AB =  

BA =    

 AB and  BA are not Commutative under Multiplication 

QUESTION 9

Define Symmetric and Skew Symmetric Matrices

Sol:

Symmetric Matrix: Let A be any square matrix, if A^T = A, then A is called Symmetric Matrix

Skew Symmetric Matrix: Let A be any square matrix if A^T = –A, then A is called Skew Symmetric Matrix

QUESTION 10

If A =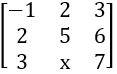 is a symmetric matrix, then find x.

Sol: Given, A = 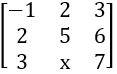 is a symmetric matrix

       ⟹ A^T = A

          ⟹ x = 6

QUESTION 11

If A =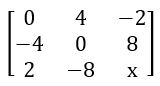 is a skew-symmetric matrix, then find x

Sol: Given A = 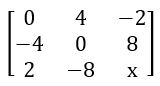is a skew-symmetric matrix

       ⟹ A^T = – A

        ⟹ x = –x

        x+ x = 0 ⟹ 2x = 0

     ⟹ x = 0

QUESTION 12

If A = and B = , then find (A B^T) ^T

Sol: Given A =    B =

   B^T =    

   (A B^T) =    

                =

(A B^T) ^T =

QUESTION 13

If A =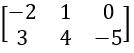 and B = , then find A + B^T

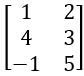Sol: Given A =  and B =

 B^T =

A + B^T = +

QUESTION 14

If A = , then show that AA^T = A^TA = I

Sol: Given A =

  A^T =

AA^T =

=

 =  

A^TA =

        =

       =

∴ AA^T = A^TA = I

QUESTION 15

Find the minor of – 1 and 3 in the matrix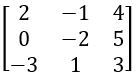

Sol: Given Matrix is

       minor of – 1 =  = 0 + 15 = 15

     minor of 3 =  = – 4 + 0 = – 4

QUESTION 16

Find the cofactors 0f 2, – 5 in the matrix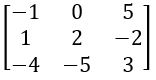

Sol: Given matrix is

 Cofactor of 2 = (–1)^{2 + 2} = –3 + 20 = 17

  Cofactor of – 5 = (–1)^{3 + 2}  = –1(2 – 5) = –1(–3) = 3

QUESTION 17

If ω is a complex cube root of unity, then show that 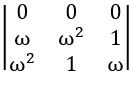= 0(where 1 + ω+ω² = 0)

Given matrix is   

   R₁ → R₁ + R₂ + R₃

 = 0 (∵ 1 + ω+ω² = 0)

QUESTION 18

If A = 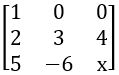and det A = 45, then find x.

Sol: Given A =

Det A = 45

⟹ = 45

   ⟹ 1(3x + 24) – 0 (2x – 20) + 0 (– 12 – 15) = 45

 ⟹ 3x + 24 = 45

        3x = 45 – 24

        3x = 21

         x = 7

QUESTION 19

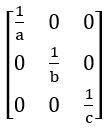
Find the adjoint and inverse of the following matrices

(i)

A =

Adj A =

A^-1 =

       =

   ∴ A^-1 =

(ii)

A =

Adj A =

A^-1 =

 ∴ A^-1 =    

QUESTION 20

Find the inverse of (abc ≠ 0)

Sol: Let A =

        Det A = a (bc – 0) – 0(0 – 0) + 0(0 – 0)

        Det A = abc ≠ 0

Cofactor matrix of A =

Adj A = (Cofactor matrix of A) ^T

           =

A^-1 =

  A^-1 =

 ∴ A^-1 = 

QUESTION 20

Find the rank of the following matrices.

(i)

Let A =

Det A = 1 (0 – 2) – 2(1 – 0) + 1(– 1 – 0)

           = – 2– 2– 1

           = – 5 ≠ 0

∴ Rank of A = 3

(ii)

Let A =

Det A = – 1 (24 – 25) + 2(18 – 20) + – 3(15 – 16)

           = – 1– 4 + 3

           = – 0

Sub matrix of A =

      Let B =

       Det B = – 4 + 6 = 2 ≠ 0

          ∴ Rank of A = 2

(iii)

Let A =

Sub matrix of A =

Det of Sub matrix of A = – 1 – 0 = – 1 ≠ 0

      ∴ Rank of A = 2

(iv)

Let A =

Sub matrix of A =

Det of Sub matrix of A =1 (1 – 0) – 0(0 – 0) + 0(0 – 0)

                                           = 1≠ 0

      ∴ Rank of A = 3

Visit my Youtube Channel: Click on Below Logo