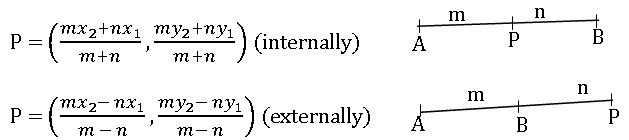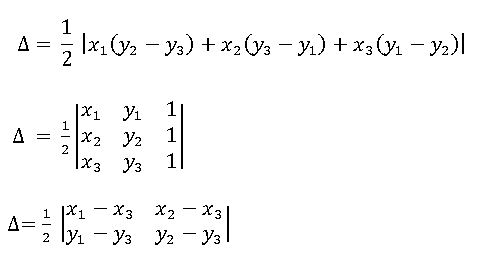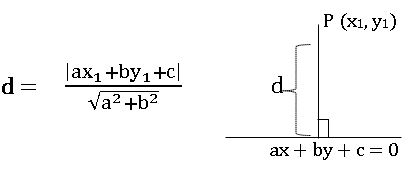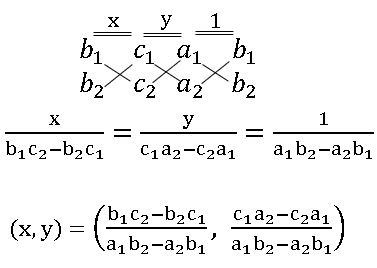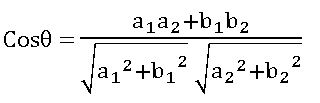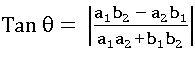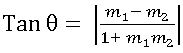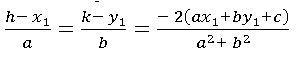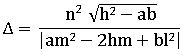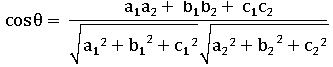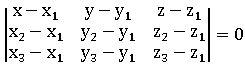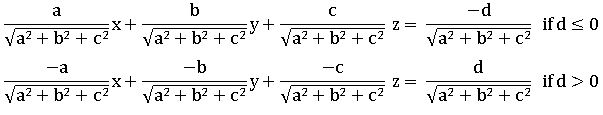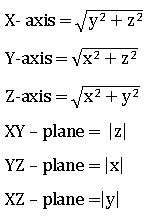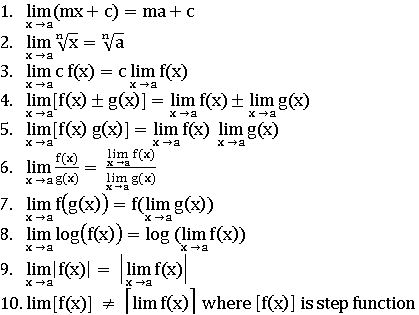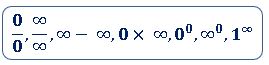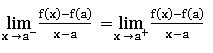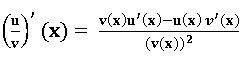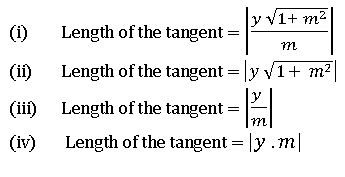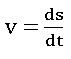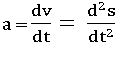TS Inter Maths 1B Concept
Ts Inter Maths 1B Concept: designed by the ‘Basics in Maths’ team. These notes to do help the TS intermediate first-year Maths students fall in love with mathematics and overcome the fear.
These notes cover all the topics covered in the TS I.P.E first year maths 1B syllabus and include plenty of formulae and concept to help you solve all the types of Inter Math problems asked in the I.P.E and entrance examinations.
0.COORDINATE GEOMETRY( BASICS)
- Distance between two points A(x1, y1), B(x2, y2) is
- distance between a point A(x1, y1) to the origin is
- The midpoint of two points A(x1, y1), B(x2, y2) is
- If P divides the line segment joining the points A(x1, y1), B(x2, y2) in the ratio m:n then the coordinates of P are
- Area of the triangle formed by the vertices A (x1, y1), B (x2, y2) and C (x3, y3) is
1. LOCUS
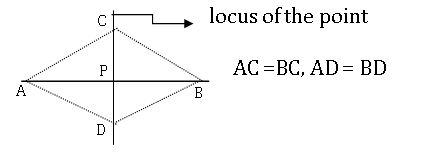
Locus: The set of points that are satisfying a given condition or property is called the locus of the point.
Ex:- If a point P is equidistant from the points A and B, then AP =BP
 Ex 2: – set of points that are at a constant distance from a fixed point.
Ex 2: – set of points that are at a constant distance from a fixed point. 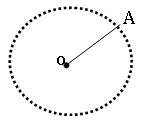
here the locus of a point is a circle.
• In a right-angled triangle PAB, the right angle at P and P is the locus of the point, then
AB2 = PA2 + PB2
•Area of the triangle formed by the vertices A (x1, y1), B (x2, y2), and C (x3, y3) is
2.CHANGE OF AXES
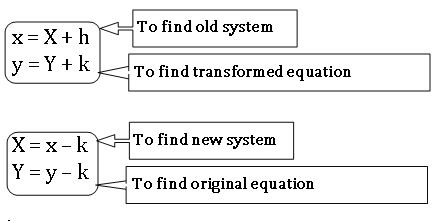
Transformation of axes:
When the origin is shifted to (h, k), without changing the direction of axes then
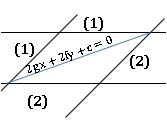
•To remove the first degree terms of the equation ax2 + 2hxy + by2 +2gx +2fy+ c = 0, origin should be shifted to the point 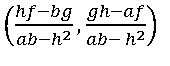
•If the equation ax2 + by2 +2gx +2fy+ c = 0, origin should be shifted to the point 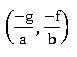
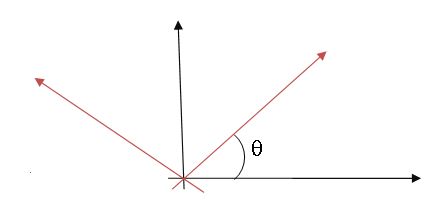
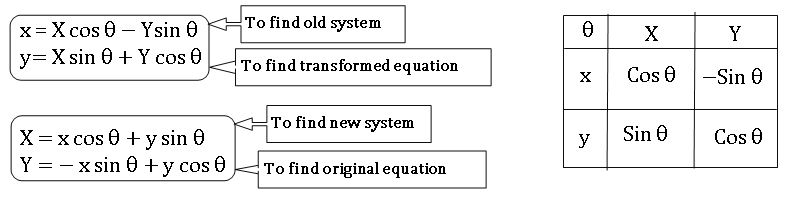
Rotation of axes:
When the axes are rotated through an angle θ then
•To remove the xy term of the equation ax2 + 2hxy + by2 = 0, axes should be rotated through an angle θ is given by
3.STRAIGHT LINES
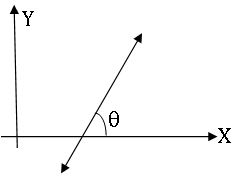
Slope:- A-line makes an angle θ with the positive direction of the X-axis, then tan θ is called the slope of the line.
m= tan θ
• The slope of the x-axis is zero.
• Slope of any line parallel to the x-axis is zero.
• The y-axis slope is undefined.
• The slope of any line parallel to the y-axis is also undefined.
• The slope of the line joining the points A (x1, y1) and B (x2, y2) is
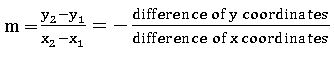 Slope of the line ax + by + c = 0 is
Slope of the line ax + by + c = 0 is 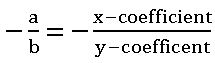
Types of the equation of a straight line:
- Equation of x- axis is y = 0.
- Equation of any line parallel to the x-axis is y = k, where k is the distance from above or below the x-axis.
- Equation of y- axis is x = 0.
- Equation of any line parallel to y-axis is x = k, where k is the distance from the left or right side of the y-axis.
Slope- intercept form
The equation of the line with slope m and y-intercept c is y = mx + c.
Slope point form:
The equation of the line passing through the point (x1, y1) with slope m is
y – y1 = m (x – x1)
Two points form:
The equation of the line passing through the points (x1, y1) and (x2, y2) ’ is
Intercept form:
The equation of the line with x-intercept a, y-intercept b is
• The equation of the line ∥ el to ax +by + c = 0 is ax +by + k = 0.
• The equation of the line ⊥ler to ax +by + c = 0 is bx −ay + k = 0.
Note: –
- If two lines are parallel then their slopes are equal
m1 = m2
- If two lines are perpendicular then product of their slopes is – 1
m1 × m2 = – 1
- The area of the triangle formed by the line ax + by + c = 0 with the coordinate axes is

- The area of the triangle formed by the line
 with the coordinate axes is
with the coordinate axes is 
Perpendicular distance (Length of the perpendicular):
The perpendicular distance from a point P (x1, y1) to the line ax + by + c = 0 is
• The perpendicular distance from origin to the line ax + by + c = 0 is 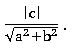
Distance between two parallel lines:
•The distance between the parallel lines ax1 + by1 + c1 = 0 and ax2 + by2 + c2 = 0 is
Perpendicular form or Normal form:
The equation of the line which is at a distance of ‘p’ from the origin and α (0≤ α ≤ 3600) is the angle made by the perpendicular with 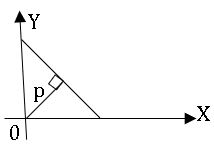 the positive direction of the x-axis is x cosα + y sinα = p.
the positive direction of the x-axis is x cosα + y sinα = p.
Symmetric form:
The equation of the line passing through point P (x1, y1) and having inclination θ is
Parametric form:
if P (x, y) is any point on the line passing through A (x1, y1) and
x = x1 + r cos θ, y = y1 + r sin θ
where ‘r’ is the distance from P to A.
• The ratio in which the line L ≡ ax + by + c = 0 divide the line segment joining the points A (x1, y1), B (x2, y2) is – L11: L22.
Where L11 = ax1 + by1 + c and L22 = ax2 + by2 + c.
Note: – the points A (x1, y1), B (x2, y2) lie on the same side or opposite side of line L = 0 according to L11 and L22 have the same sign or opposite sign.
∗ x-axis divides the line segment joining the points A (x1, y1), B (x2, y2) in the ratio – y1: y2.
∗ y-axis divides the line segment joining the points A (x1, y1), B (x2, y2) in the ratio – x1: x2.
Point of intersection of two lines:
the point of intersection of two lines a1x + b1y + c = 0 and a2x + b2y + c = 0 is
Concurrent Lines: 
Three or more lines are said to be concurrent lines if they have a point in common.
The common point is called the point of concurrence.
∗ The condition that the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 and a3x + b3y + c3 = 0 to be concurrent is
a3(b1c2 – b2c1) + b3(c1a2 – c2a1) + c3(a1b2 – a2b1).
∗ The condition that the lines ax + hy +g = 0, hx + by + f = 0 and gx +fy + c = 0 is
abc + 2fgh – af2 – bg2 – ch2 = o.
Note: – if two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 said to be identical (same) if ![]()
Family of a straight line:
Family of straight lines: – A set of straight lines having a common property is called a family of straight lines.
Let L1 ≡ a1x + b1y + c1 = 0 and L2 ≡ a2x + b2y + c2 =0 represent two intersecting lines, theThe equation λ1 L1 + λ2 L2 = 0 represent a family of straight lines passing through the point of intersection of the lines L1 = 0 and L2 = 0.
∗ The equation of the straight line passing through the point of intersection of the lines L1 = 0 and L2 = 0 is L1 + λL2 = 0.
The angle between two lines:
If θ is the angle between the lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 then
∗ If θ is an acute angle then
∗ If θ is the angle between two lines, then (π – θ) is another angle between two lines.
∗ If θ≠π/2 is angle between the lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, then
∗ If m1, m2 are the slopes of two lines then
Note: – The lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are
∗ Perpendicular iff a1a2 + b1b2 = 0
The foot of the perpendicular:
If Q (h. k) is the foot of the perpendicular from a point P (x1, y1)to the line ax + by +c = 0 then 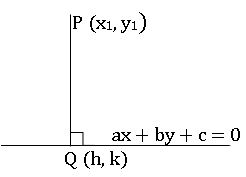
Image of the point:
If Q (h. k) is the image of point P (x1, y1) with respect to the line ax + by +c = 0 then 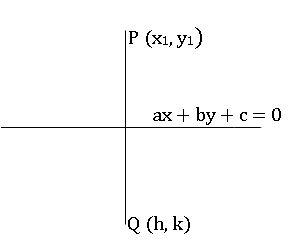
Collinear Points:
If three points are said to be collinear, then they lie on the same line.
∗ If A, B, and C are collinear, then
Slope of AB = Slope of BC (or) Slope of BC = Slope of AC (or) Slope of AB = Slope of AC
4. PAIR OF STRAIGHT LINES
∎ ax2 + 2hxy + by2 = 0 is called the second-degree homogeneous equation in two variable x and y.
This equation always represents a pair of straight lines which are passing through the origin.
∎ If l1x + m1y = 0 and l2x + m2y = 0 are two lines represented by the equation ax2 + 2hxy + by2 = 0, then ax2 + 2hxy + by2 = (l1x + m1y) (l2x + m2y)
⇒ a = l1l2; 2h = l1m2 + l2m1; b = m1m2
∎ If m1, m2 are the slopes of the lines represented by the equation ax2 + 2hxy + by2 = 0, then
m1+ m2 = – 2h/b and m1 m2 = a/b
∎ The lines represented by the equation ax2 + 2hxy + by2 = 0 are ![]()
∎ If h2 = ab, then the lines represented by the equation ax2 + 2hxy + by2 = 0 are coincident.
∎ If two lines represented by the equation ax2 + 2hxy + by2 = 0 are equally inclined to the coordinate axes then h = 0 and ab < 0.
∎ The equation of the pair of lines passing through the point (h, k) and
(i) Parallel to the lines represented by the equation ax2 + 2hxy + by2 = 0 is
a (x – h)2 + 2h (x – h) (y – k) + b (y – k)2 = 0
(ii) Perpendicular to the lines represented by the equation ax2 + 2hxy + by2 = 0 is
b (x – h)2 – 2h (x – h) (y – k) + a (y – k)2 = 0
Angle between the lines:
If θ is the angle between the lines represented by the equation ax2 + 2hxy + by2 = 0, then 
∎ If a + b = 0, then two lines are perpendicular.
Area of the triangle:
The area of the triangle formed by the lines ax2 + 2hxy + by2 = 0 and the line lx + my + n = 0 is
Angular Bisectors:
⇒ the angle between angular bisectors is always 900
L1 = o, L2 = o are two non-parallel lines the locus of the point P such that the perpendicular distance from P to the first lie is equal to the perpendicular distance from P to second line is called the angular bisector of two lines.
⇒ If two lines are a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, then the angular bisectors are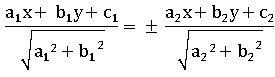
∎ The equation of the pair of angular bisectors of ax2 + 2hxy + by2 = 0 is
h (x2 – y2) = (a – b =) xy.
∎ If ax2 + 2hxy + by2 + 2gx 2fy + c= 0 represents a pair of straight lines then
(i) abc + 2fgh – af2 – bg2 – ch2 = 0
(ii) h2 ≥ ab, g2 ≥ ac and f2 ≥ bc
⇒ If two lines represented by ax2 + 2hxy + by2 + 2gx 2fy + c= 0 are
l1x + m1y + n1 = 0 and l2x + m2y + n2 = 0, then
ax2 + 2hxy + by2 + 2gx 2fy + c = (l1x + m1y + n1) (l2x + m2y + n2)
a = l1l2; 2h = l1m2 + l2m1; b = m1m2 ; 2g = l1n2 + l2n1; 2f = m1n2 + m2n1 and c = n1n2
⇒ The point of intersection of the lines represented by ax2 + 2hxy + by2 + 2gx 2fy + c= 0 is 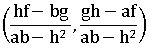
∎ If two line have same homogeneous path then the lines represented by the first pair is parallel to the lines represented by the second pair.
ax2 + 2hxy + by2 + 2gx 2fy + c= 0 …………… (2)
ax2 + 2hxy + by2 = 0 …………… (1)
equation (1) and equation (2) form a parallelogram, one of the diagonals of parallelogram which is not passing through origin is 2gx + 2fy + c = 0.
∎ If two lines represented by ax2 + 2hxy + by2 + 2gx 2fy + c= 0 are parallel then
- h2 = ab (ii) af2 = bg2 (iii) hf = bg, gh = ab
⇒ Distance between parallel lines is 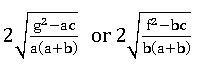
5. THREE DIMENSIONAL COORDINATES
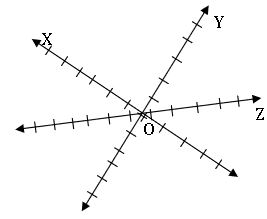
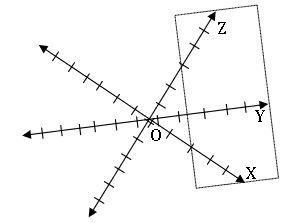
• Let X’OX, Y’OY be two mutually perpendicular lines passing through a fixed point ‘O’. These two lines determine the XOY – plane (XY- plane). Draw the line Z’OZ perpendicular to XY – plane and passing through ‘O’.
The fixed point ‘O’ is called origin and three mutually perpendicular lines X’OX, Y’OY, Z’OZ are called Rectangular coordinate axes.
Three coordinate axes taken two at a time determine three planes namely XOY- plane, YOZ-plane, ZOY-plane or XY-plane, YZ-plane, ZX-plane respectively.
For every point P in space, we can associate an ordered triad (x, y, z) of real numbers formed by its coordinates.
The set of points in space is referred to as ‘Three-Dimensional Space’ or R3– Space.
∗ If P (x, y, z) is a point in a space, then
x is called x-coordinate of P
y is called y-coordinate of P
z is called z-coordinate of P
Distance between two points in space:
∗ Distance between the points A (x1, y1, z1) and B (x2, y2, z2) is ![]()
∗ Distance between the point P (x, y, z) to the origin is ![]()
Translation of axes:
When the origin is shifted to the point (h, k, l), then
X = x – h; Y = y – k; Z = z – l and x = X + h; y = Y + k; z = Z + l
∗ The foot of the perpendicular from P (x, y, z) to X-axis is A (x, 0, 0).
The perpendicular distance of P from X-axis is ![]()
Similarly,
The perpendicular distance of P from Y-axis is ![]()
The perpendicular distance of P from Z-axis is ![]()
Collinear points: If three or more points lie on the same line are called collinear points.
Section formula:
The point dividing the line segment joining the points A (x1, y1, z1) and B (x2, y2, z2) in the ratio m : n is given by ![]()
The mid-point of the line segment joining the points A (x1, y1, z1) and B (x2, y2, z2) is ![]()
The centroid of the triangle whose vertices are A (x1, y1, z1), B (x2, y2, z2) and C (x3, y3, z3) is ![]()
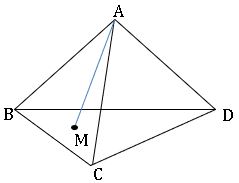
→ It has 4 vertices and 6 edges.
→ A Tetrahedron is a closed figure formed by four planes not all passing through the same point.
→ Each edge arises as the line of intersection of two of the four planes.
→ The line segment joining the vertices to the centroid of opposite face. The point of concurrence is called centroid of Tetrahedron.
→ Centroid divides the line segment in the ratio 3:1.
→ The centroid of the Tetrahedron whose vertices are A (x1, y1, z1), B (x2, y2, z2), C (x3, y3, z3) and C (x4, y4, z4) is ![]()
The line segment joining the points (x1, y1, z1), (x2, y2, z2) is divided by
XY – plane in the ratio – z1: z2
YZ – plane in the ratio – x1: x2
XZ – plane in the ratio – y1: y2
6. DIRECTION COSINES AND RATIOS
Consider a ray OP passing through origin ‘O’ and making angles α, β, γ respectively with the positive direction of X, Y, Z axes.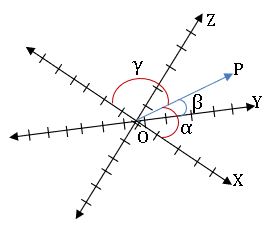
Cos α, Cos β, Cos γ are called Direction Cosines (dc’s) of the ray OP.
Dc’s are denoted by (l, m, n), where l = Cos α, m = Cos β, n = Cos γ
• A line in a space has two directions, it has two sets of dc’s, one for each direction. If (l, m, n) is one set of dc’s, then (-l, -m, -n) is the other set.
• Suppose P (x, y, z) is any point in space such that OP = r. If (l, m, n) are dc’s of a ray OP then x = lr, y= mr, z = nr.
• If OP = r and dc’s of OP are (l, m, n) then the coordinates of P are (lr, mr, nr).
• If P (x, y, z) is a point in the space, then dc’s of OP are 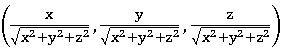
• If (l, m, n) are dc’s of a line then l2 + m2 + n2 = 1.
⇒ cos2α + cos2β + cos2γ = 1.
Direction Ratios:
Any three real numbers which are proportional to the dc’s of a line are called direction ratios (dr’s) of that line.
• Let (a, b, c) be dr’s of a line whose dc’s are (l, m, n). Then (a, b, c) are proportional to (l, m, n) ![]()
and a2 + b2 + c2 ≠ 1.
• Dr’s of the line joining the points (x1, y1, z1), (x2, y2, z2) are (x2 – x1, y2 – y1, z2 – z1)
• If (a, b, c) are dr’s of a line then its dc’s are ![]()
• If (l1, m1, n1), (l2, m2, n2) are dc’s of two lines and θ is angle between them then Cos θ = l1l2 + m1m2 + n1n2
If two lines perpendicular then l1l2 + m1m2 + n1n2 = 0.
• If (a1, b1, c1), (a2, b2, c2) are dr’s of two lines and θ is the angle between them then
If two line are perpendicular then a1a2 + b1b2 + c1c2 = 0.
7. THE PLANE
Plane: A plane is a proper subset of R3 which has at least three non-collinear points and any two points in it.
∎ Equation of the plane passing through a given point A (x1, y1, z1), and perpendicular to the line whose dr’s (a, b, c) is a(x – x1) + a(y – y1) + a(z – z1) = 0.
∎ The equation of the plane hose dc’s of the normal to the plane (l, m, n) and perpendicular distance from the origin to the pane p is lx + my + nz = p
∎ The equation of the plane passing through three non-collinear points A (x1, y1, z1), B (x2, y2, z2) and C (x3, y3, z3) is
∎ The general equation of the plane is ax + by + cz + d = 0, where (a, b, c) are Dr’s of the normal to the plane.
Normal form:
The equation of the plane ax + by + cz + d = 0 in the normal form is
Perpendicular distance:
The perpendicular distance from (x1, y1, z1) to the plane ax + by + cz + d = 0 is 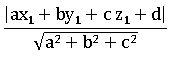
The perpendicular distance from the origin to the plane ax + by + cz + d = 0 is
X- intercept = aIf a plane cuts X –axis at (a, 0, 0), Y-axis at (0, b, 0) and Z-axis at (0, 0, c) then
Y-intercept = b
Z-intercept = c
The equation of the plane in the intercept form is ![]()
The intercepts of the plane ax + by + cz + d =0 is -d/a, -d/b, -d/c
∎ The equation of the plane parallel to ax + by + cz + d = 0 is ax + by + cz + k = 0.
∎ The equation of XY – plane is z = 0.
∎ The equation of YZ – plane is x = 0.
∎ The equation of XZ – plane is y = 0.
∎ Distance between the two parallel planes ax + by + cz + d1 =0 and ax + by + cz + d2 =0 is 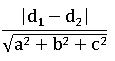
The angle between two planes:
The angle between the normal to two planes is called the angle between the planes.
If θ is the angle between the planes a1 x + b1 y + c1 z + d1 =0 and a2 x + b2 y + c2 z + d2 =0 then
If two line are perpendicular then a1a2 + b1b2 + c1c2 = 0.
∎ The distance of the point P (x, y, z) from
8. LIMITS AND CONTINUITY
Intervals:
Let (a, b) ∈ R such that a ≤ b, then the set
- {x ∈ R: a ≤ x ≤ b}, is denoted by [a, b] and it is called as closed interval
- {x ∈ R: a < x < b}, is denoted by (a, b) and it is called as open interval
- {x ∈ R: a < x ≤ b}, is denoted by (a, b] and it is called as open closed interval
- {x ∈ R: a ≤ x < b}, is denoted by [a, b) and it is called as closed open interval
- {x ∈ R: x ≥ a}, is denoted by [a, ∞)
- {x ∈ R: x > a}, is denoted by (a, ∞)
- {x ∈ R: x ≤ a}, is denoted by (- ∞, a]
- x ∈ R: x < a}, is denoted by (- ∞, a)
Neighbourhood:
Let a ∈ R. If δ > 0, then the open interval (a – δ, a + δ) is called the δ – neighbourhood of ‘a’
Limit:
If f(x) is a function of x such that if x approaches to a constant value ‘a’, then the value of f(x) also approaches to ‘l’. Then the constant ‘I’ is called a limit of f(x) at x = a
Or
A real number l is called the limit of the function f, if for all ϵ> 0 there exist δ > 0 such that ![]() whenever
whenever![]() ⟹
⟹ ![]()
Properties of Limits:
Sand witch theorem:( Squeez Principle):
f, g, and h are functions such that f(x) ≤ g(x) ≤ h(x), then ![]() and if
and if ![]()
Left- hand and Right-hand Limits:
If x < a, then is ![]() called left-hand limit
called left-hand limit
If x > a, then ![]() is called right-hand limit
is called right-hand limit
Note:
In Determinate forms:
if a function f(x) any of the following forms at x = a:
Then f(x) is said to be indeterminate at x = a.
Continuity:
Condition 1: If the condition is like x = a and x ≠ a, then we use following property.
If ![]() then f(x) is continuous at x = a, otherwise f(x) is not continuous.
then f(x) is continuous at x = a, otherwise f(x) is not continuous.
Condition 2: If the condition is like x ≤ a and x >a, or x < a and x ≥a then we use following property.
If ![]() then f(x) is continuous at x = a, otherwise f(x) is not continuous.
then f(x) is continuous at x = a, otherwise f(x) is not continuous.
9.DIFFERENTIATION
Let f be a function defined on a neighbourhood of a real number ‘a’ if ![]() exist then we say that f is differentiable at x a and it is denoted by f'(a).
exist then we say that f is differentiable at x a and it is denoted by f'(a).
∎ If right hand derivative = left hand derivative, then f is differentiable at ‘a’.
First principle in derivative:
The first principle of the derivative of f at any real number ‘x’ is f’(x) = ![]()
∎ The differentiation of f(x) is denoted by ![]()
![]() means differentiation of ‘y’ with respect to ‘x’
means differentiation of ‘y’ with respect to ‘x’
∎ The derivative of constant function is zero i.e., f’(a) = 0 where ‘a’ is any constant.
∎ Let I be an interval in R u and v are real valued functions on I and x ∈ I. Suppose that u and v are differentiable at ‘x’, then
- (u ± v) is also differentiable at ‘x’ and (u ± v)’(x) = u’ (x) ± v’(x).
- ‘uv’ is also differentiable at ‘x’ and (uv)’(x) = u(x) v’(x) + v(x) u’(x).
- αu + βv is also differentiable at ‘x’ and (αu + βv)’(x) = αu’(x) + βv’(x), α, β are constants.
 is also differentiable at ‘x’ and
is also differentiable at ‘x’ and 
∎ (f o g)’ (x) = f’(g(x)). g’(x).
Formulae:
Derivative of Trigonometric & Inverse trigonometric functions:
Derivative of Hyperbolic & Inverse Hyperbolic functions:
Parametric Differentiation:
If x = f(t) and y = g(t) then the procedure of finding in terms of the parameter ‘t’ is called parametric equations. 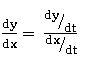
Implicitly differentiation:
An equation involving two or more variables is called an implicit equation.
ax2 + 2hxy + b y2 = 0 is an implicit equation in terms of x and y.
The process of finding ![]() from an implicit equation is called implicitly differentiation.
from an implicit equation is called implicitly differentiation.
Derivative of one function w.r.t. another function:
The derivative of f(x) w.r.t g(x) is 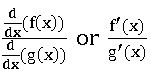
Second order derivative:
Let y = f(x) be a function, if y is differentiable then the derivative of f is f’(x). If ‘(x) is again differentiable then the derivative of f’(x) is called second order derivative. And it is denoted by f” (x) or ![]()
APPLICATION OF DERIVATIVES
10. ERRORS AND APPROXIMATIONS
Approximations:
Let y f(x) be a function defined an interval I and x ∈ I. If ∆x is any change in x, then ∆y be the corresponding change in y thus ∆y = f (x + ∆x) – f (x).
For ‘ϵ.∆x’ is very small and hence, 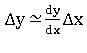
Approximate value is f (x + ∆x) = f(x) + f’(x). ∆x
Differential:
Let y f(x) be a function defined an interval I and x ∈ I. If ∆x is any change in x, then![]() called differential of y = f(x) and it is denoted by df.
called differential of y = f(x) and it is denoted by df.
∴ dy = f’(x). ∆x
Errors:
Let y f(x) be a function defined an interval I and x ∈ I. If ∆x is any change in x, then ∆y be the corresponding change in y.
The Following formulae will be used in Solving problems
If ‘r’ is radius, ‘d’ is diameter ‘P’ is the perimeter or circumference and A is area of the circle then
d= 2r, P = 2πr = πd and A = πr2sq.u
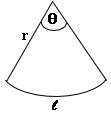
If ‘r’ is the radius, ‘l’ is the length of arc and θ is of the sector then
Area = ½ l r = ½ r2θsq.u.
Perimeter = l + 2r = r (θ + 2) u.
Length of the Arc ‘l’ = rθ (θ must be in radians).
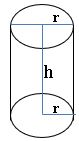
If ‘r is the radius of the base of cylinder and ‘h’ is the height of the cylinder, then
Area of base = πr2 sq.units.
Lateral surface area = 2πrh units.
Total surface area = 2πr (h + r) units.
Volume = πr2 h cubic units.
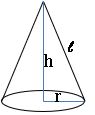
If ‘r’ is the radius of base, ‘h’ is the height of cone and ‘l’ is slant height then
l 2 + r2 = h2
Lateral surface area = πrl units.
Total surface area = πr (l + r) sq. units.
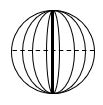
If ‘r’ is the radius of the Sphere then
Surface area = πr2 sq. units.
11. TANGENTS AND NORMALS
Tangent of a Curve: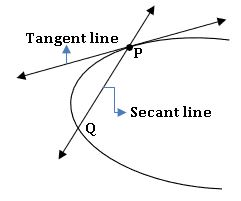
If the secant line PQ approaches to the same position as Q moves along the curve and approaches to either side then limiting position is called a ‘Tangent line’ to the curve at P. The point P is called point of contact
Let y = f(x) be a curve, P a point on the curve. If Q(≠P) is another point on the curve then the line PD is called secant line.
Gradient of a curve:
Let y = f(x) be a curve and P (x, y) be a point on the curve. The slope of the tangent to the curve y = f(x) at P is called gradient of the curve.
Slope of the tangent to the curve y = f(x) at P (x, y) is m = 
∎ The equation of the tangent at P (x1, y1) to the curve is y – y1 = m (x – x1) where m =
Let y = f(x) be a curve and P (x, y) be a point on the curve. The line passing through P and perpendicular to the tangent of the curve y = f(x) at P is called Normal of the curve.
∎ The equation of the tangent at P (x1, y1) to the curve is y – y1 = -1/m (x – x1).
Slope of the normal is -1/m. where m =
Lengths of tangent, normal, subtangent and subnormal: 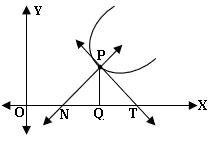
PT → Normal; QN → subnormal
PN → Tangent; QT → subtangent
Angle between two curves:
If two curves intersect at a point P., then the angle between the tangents of the curves at P is called the angle between the curves at P.
∎ If m1, m2 are the slopes of two tangents of the two curves and θ is the angle between the curves then
Note:
- If m1= m2, then two corves are touch each other.
- if m1× m2 = –1, then two curves intersect orthogonally.
12. RATE MEASURE
Average rate of change:
if y = f(x) then the average rate of change in y between x = x1 and x = x2 is defined as 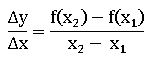
Instantaneous rate of change:
if y = f(x), then the instantaneous rate of change of a unction f at x = x0 is defined as 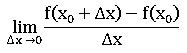
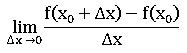
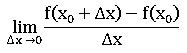
Rectilinear Motion:
A motion of a particle in a line is called Rectilinear motion. The rectilinear motion is denoted by s = f(t) where f(t) is the rule connecting ‘s’ and ‘t’.
Velocity, Acceleration:
A particle starts from a fixed point and moves a distance ‘S’ along a straight-line during time ‘t’ then
Note:
(i) If v> 0, then the particle s moving away from the straight point.
(ii) If v < 0, then particle s moving away towards the straight point.
(iii) If v = 0, then the particle comes rest.
13.ROLLE’S & LANGRANGEE’S THEOREM
Rolle’s Theorem:
Suppose a, b (a < b) are two real numbers. Let f: [a, b] → R be a function satisfying the following conditions:
(i) f is continuous on [a, b]
(ii) f is differentiable on (a, b) and
(iii) f(a) = f(b)
then there exists at least one c ∈ (a, b) such that f’(c)= 0.
Lagrange’s Theorem:
Suppose a, b (a < b) are two real numbers. Let f: [a, b] → R be a function satisfying the following conditions:
(i) f is continuous on [a, b]
(ii) f is differentiable on (a, b) and
then there exists at least one c ∈ (a, b) such that f’(c)= 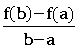
14.INCREASING & DECREASING FUNCTIONS
⨂ Let f be a real function on an interval I then f is said to be
(i) an increasing function on I if
x1 < x2 ⇒ f (x1) ≤ f (x2) ∀ x1, x2 ∈ I
(ii) decreasing function on I if
x1 < x2 ⇒ f (x1) ≥ f (x2) ∀ x1, x2 ∈ I
⨂ Let f be a real function on an interval I then f is said to be
(i) strictly increasing function on I if
x1 < x2 ⇒ f (x1) < f (x2) ∀ x1, x2 ∈ I
(ii) strictly decreasing function on I if
x1 < x2 ⇒ f (x1) > f (x2) ∀ x1, x2 ∈ I
⨂ Let f(x) be a real valued function defined on I = (a, b) or [a, b) or (a, b] or [a, b]. Suppose f is continuous on I and differentiable in (a, b). If
(i) f’ (c) > 0 ∀ c ∈ (a, b), then f is strictly increasing on I
(ii) f’ (c) < 0 ∀ c ∈ (a, b), then f is strictly decreasing on I
(iii) f’ (c) ≥ 0 ∀ c ∈ (a, b), then f is increasing on I
(iv) f’ (c) ≤ 0 ∀ c ∈ (a, b), then f is decreasing on I
Critical point:
A point x = c in the domain of the function said to be ‘critical point’ of the function f if either f’ (c) = 0 or f’ (c) does not exists.
Stationary point:
A point x = c in the domain of the function said to be ‘stationary point’ of the function f if f’ (c) = 0.
MAXIMA & MINIMA
Global maxima – Global minima:
Let D be an interval in R and f: D → R be a real function and c ∈ D. Then f is said to be
(i) a global maximum on D if f(c) ≥ f(x)
(ii) a global minimum on D if f(c) ≤ f(x)
Relative maximum:
Let D be an interval in R and f: D → R be a real function and c ∈ D. Then f is said to be relative maximum at c if there exist δ > 0 such that f(c) ≥ f(x) ∀ x ∈ (c – δ, c + δ).
Here, f (c) is called relative maximum value of f(x) at x = c and the point x = c is called point of relative maximum.
Relative minimum:
Let D be an interval in R and f: D → R be a real function and c ∈ D. Then f is said to be relative maximum at c if there exist δ > 0 such that f(c) ≤ f(x) ∀ x ∈ (c – δ, c + δ).
Here, f (c) is called relative maximum value of f(x) at x = c and the point x = c is called point of relative minimum.
⨂ The relative maximum and minimum value of f are called extreme values.
⨂ If f is either minima or maxima f’ (α) = 0.
⨂ Let f be a continuous function om [a, b] and α ∈ (a, b)
(i) If f’ (α) = 0 and f’’ (α) >0, then f(α) is relative minimum.
(ii) if f’ (α) = 0 and f’’ (α) <0, then f(α) is relative maximum
My App: Click Here
Visit My Youtube Channel: Click on below logo