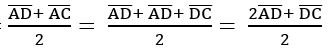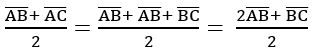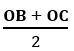Addition of Vectors
These solutions were designed by the ‘Basics in Maths’ team. These notes to do help intermediate First-year Maths students.
Inter Maths – 1A two marks questions and solutions are very useful in IPE examinations.
Addition of Vectors
QUESTION 1
Find the unit vector in the direction of 
Sol: Given vector is
The unit vector in the direction of a vector 
is given by
QUESTION 2
Find a vector in the direction of a where 
that has a magnitude of 7 units.
Sol: Given vector is
The unit vector in the direction of a vector is 
The vector having the magnitude 7 and in the direction of is
QUESTION 3
Find the unit vector in the direction of the sum of the vectors, a = 2i + 2j – 5k and b = 2i + j + 3k
Sol Given vectors are a = 2i + 2j – 5k and b = 2i + j + 3k
a + b = (2i + 2j – 5k) + (2i + j + 3k) = 4i + 3j – 2k
QUESTION 4
Write the direction cosines of the vector 
Sol: Given vector is
∴ Direction cosines are 
QUESTION 5
Show that the points whose position vectors are – 2a + 3b + 5c, a + 2b + 3c, 7 a – c are collinear when a, b, c are non-collinear vectors
Sol: Let OA = – 2a + 3b + 5c, OB = a + 2b + 3c, OC = 7 a – cA
B = OB – OA = a + 2b + 3c – (– 2a + 3b + 5c)
AB = 3a – b – 2c
AC = OC – OA = 7 a – c – (– 2a + 3b + 5c)
AC = 9a – 3b – 6c = 3(3a – b – 2c)
AC = 3 AB
A, B and C are collinear
QUESTION 6
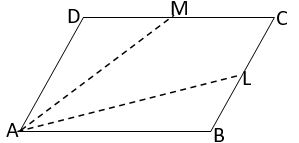
ABCD is a parallelogram if L and M are middle points of BC and CD. Then find (i) AL and AM in terms of AB and AD (ii) 𝛌, if AM = 𝛌 AD – LM
Sol: Given, ABCD is a parallelogram and L and M are middle points of BC and CD
(i) Take A as the origin
M is the midpoint of CD
AM =
= AD + ½ AB (∵ AB = DC)
L is the midpoint of BC
AL =
= AB + ½ AD ((∵ BC = AD)
(ii) AM = 𝛌 AD – LM
AM + LM= 𝛌 AD
AD + ½ AB + AD + ½ AB – (AB + ½ AD) = 𝛌 AD
AD + ½ AB + AD + ½ AB – AB – ½ AD = 𝛌 AD
3/2 AD = 𝛌 AD
∴𝛌 = 3/2
QUESTION 7
If G is the centroid of the triangle ABC, then show that OG = 
when,
are the position vectors of the vertices of triangle ABC.
Sol: OA = a, OB = b, OC = c and OD = d
D is the midpoint of BC
OD = 
G divides median AD in the ratio 2: 1
OG =
∴ OG =
QUESTION 8
If = 
, = 
are collinear vectors, then find m and n.
Sol: Given , are collinear vectors
⟹ = λ
Equating like vectors
2 = 4 λ; 5 = m λ; 1 = n λ
λ =
5 = m ⟹ m =10
1 = n ⟹ n = 2
∴ m = 10, n = 2
QUESTION 9
Let If 
, 
. Find the unit vector in the direction of a + b.
Sol: Given vectors are and
a + b = 
The unit vector in the direction of a + b = 
= 
= 
QUESTION 10
If the vectors – 3i + 4j + λk and μi + 8j + 6k. are collinear vectors, then find λ and μ.
Sol: let a = – 3i + 4j + λk, b = μi + 8j + 6k
⟹ a = tb
– 3i + 4j + λk = t (μi + 8j + 6k)
– 3i + 4j + λk = μt i + 8t j + 6t k
Equating like vectors
– 3 = μt; 4 = 8t, λ = 6t
4 = 8t
t =
– 3 = μ ⟹μ=– 6
λ = 6 ⟹ λ = 3
∴ μ=– 6, λ = 3
QUESTION 11
ABCD is a pentagon. If the sum of the vectors AB, AE, BC, DC, ED and AC is 𝛌 AC then find the value of 𝛌
Sol: Given, ABCD is a pentagon
AB + AE + BC + + DC + ED + AC = 𝛌 AC
(AB + BC) + (AE + DC + ED) + AC = 𝛌 AC
AC + AC + AC = 𝛌 AC
3 AC = 𝛌 AC
𝛌 = 3
QUESTION 12
If the position vectors of the points A, B and C are – 2i + j – k and –4i + 2j + 2k and 6i – 3j – 13k respectively and AB = 𝛌 AC, then find the value of 𝛌
Sol: Given, OA = – 2i + j – k , OB = –4i + 2j + 2k and OC = 6i – 3j – 13k
AB = OB – OA = –4i + 2j + 2k – (– 2i + j – k)
= –4i + 2j + 2k +2i – j + k
= –2i + j + 3k
AC = OC – OA = 6i – 3j – 13k – (– 2i + j – k)
= 6i – 3j – 13k +2i – j + k
= 8i –4 j –12k
= – 4 (2i + j + 3k)
AC = – 4 AB
Given AB = 𝛌 AC
𝛌 = – 1/4
QUESTION 13
If OA = i + j +k, AB = 3i – 2j + k, BC = i + 2j – 2k, CD = 2i + j +3k then find the vector OD
Sol: Given OA = i + j +k, AB = 3i – 2j + k, BC = i + 2j – 2k, CD = 2i + j +3k
OD = OA + AB + BC + CD
= i + j +k + 3i – 2j + k + i + 2j – 2k + 2i + j +3k
= 7i + 2j +4k
QUESTION 14
Let a = 2i +4 j –5 k, b = i + j+ k, c = j +2 k, then find the unit vector in the opposite direction of a + b + c
Sol: Given, a = 2i +4 j –5 k, b = i + j+ k, c = j +2 k
a + b + c = 2i +4 j –5 k + i + j+ k + j +2 k
= 3i +6j –2k
The unit vector in the opposite direction of a + b + c is 
⟹ 
=
QUESTION 15
Is the triangle formed by the vectors 3i +5j +2k, 2i –3j –5k, –5i – 2j +3k
Sol: Let a =3i +5j +2k, b = 2i –3j –5k, c = –5i – 2j +3k
∴ Given vectors form an equilateral triangle.
QUESTION 16
Using the vector equation of the straight line passing through two points, prove that the points whose position vectors are a, b, (3a – 2b) are collinear.
Sol: the vector equation of the straight line passing through two points a, b is
r = (1 – t) a+ t b
3a – 2b = (1 – t) a+ t b
Equating like vectors
1 – t = 3 and t = – 2
∴ Given points are collinear.
QUESTION 17
OABC is a parallelogram If OA = a and OC = c, then find the vector equation of the side BC
Sol: Given, OABC is a parallelogram and OA = a, OC = c
The vector equation of BC is a line which is passing through C(c) and parallel to OA
⟹ the vector equation of BC is r = c + t a
QUESTION 18
If a, b, c are the position vectors of the vertices A, B, and C respectively of triangle ABC, then find the vector equation of the median through the vertex A
Sol: Given OA = a, OB = b, OC = c
D is mid of BC
OD =
= 
The equation of AD is
r = (1 – t) a + t ( )
QUESTION 19
Find the vector equation of the line passing through the point 2i +3j +k and parallel to the vector 4i – 2j + 3k
Sol: Let a =2i +3j +k, b = 4i – 2j + 3k
The vector equation of the line passing through a and parallel to the vector b is r = a + tb
r = 2i +3j +k + t (4i – 2j + 3k)
= (2 + 4t) i + (3 – 2t) j + (1 + 3t) k
QUESTION 20
Find the vector equation of the plane passing through the points i – 2j + 5k, – 2j –k and – 3i + 5j
Sol: The vector equation of the line passing through a, b and cis r = (1 – t – s) a + tb + sc
⟹ r = (1 – t – s) (i – 2j + 5k) + t (– 2j –k) + s (– 3i + 5j)
= (1 – t – 4s) i + (– 2 – 3t + 7s) j + (5 – 6t – 5s) k
Visit my Youtube Channel: Click on Below Logo
