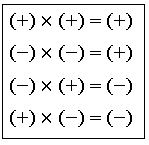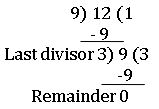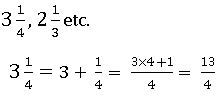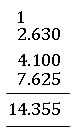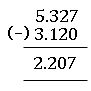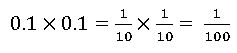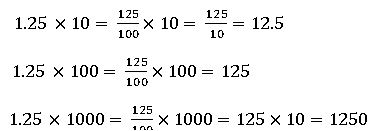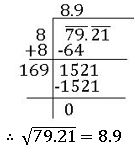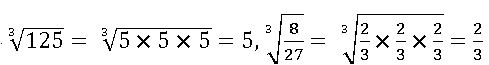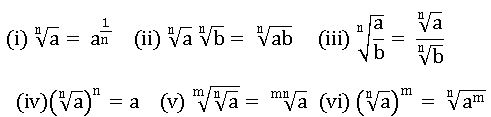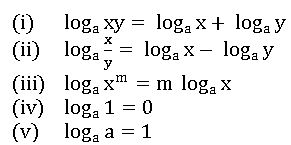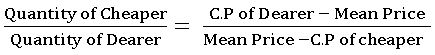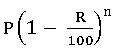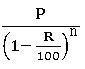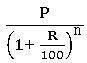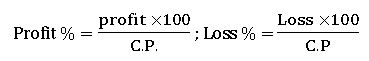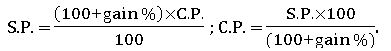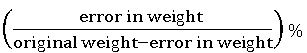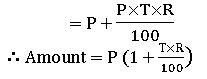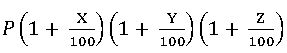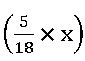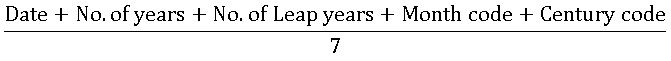Quantitative Aptitude For Competitive Exams
Quantitative Aptitude
This Topic written by the ‘Basics in Maths’ team. These notes to do help the students with any Competitive Exam.

These notes cover all the topics covered in any Competitive Exam syllabus and include plenty of formulae and concepts to help you solve all the Competitive examinations.
Quantitative Aptitude Number System
Number: A number is a mathematical object used to count and measure.1,2,3……. etc.
the ten thousand places in 5432 are greater than that in 4978.
Order of numbers
Ascending Order: arrange the numbers from smallest to the greatest; this order is called Ascending order.
Ex: – 23, 44, 65, 79, 100
Descending Order: arrange the numbers from greatest to the smallest, this order is called Ascending order. Ex: – 100,79, 65, 33, 23
Formations of numbers
Form the largest and smallest possible numbers using the digits 3, 2, 4, 1 without repetition:
The largest number formed by arranging the given digits in descending order _ 4321.
The smallest number formed by arranging the given digits in ascending order _ 1234.
The greatest two-digit number is 99.
The greatest three-digit number is 999.
The greatest four-digit number is 9999.
Place value
Place value is the positional notation, which defines a digit’s position.
Ex: – 1234 ⟶ 4 is one’s place, 3 is tens place, 2 in the hundreds place and 1 is thousands place.
Face value
The face value of a digit in a numeral is its own value.
Ex: – 1234
Face value of r is 200
Face value of 3 is 30
Place value table for Indian system:

Indian system of numeration: – in the Indian system of numeration we use ones, tens, hundreds, thousands, lakhs, and crores. The first comma comes after three digits from the right, the second comma comes two digits later and the third comma comes after another two digits.
Ex: – “three crores thirty-five lakh seventeen thousand four hundred thirty” can be written as 3,35,17,430
The international system of numeration: – In an International system of numeration we use ones, tens, hundreds, thousands, millions, and billions.
Ex: – “six hundred thirty-five million two hundred eighteen thousand nine hundred twenty-four” can be written as 635,218,924.
Types of Numbers:
Natural numbers: All the counting numbers starting from 1 are called Natural numbers.
1, 2, 3…
Whole numbers: Whole numbers are the collection of natural numbers.
0, 1, 2, 3 …
Note: All natural numbers are whole numbers but all whole numbers need not be natural numbers.
Integers: integers are the collection of whole numbers and negative numbers.
…., -3, -2, -1, 0, 1, 2, 3….
Rational numbers: The numbers which are written in the form of, where p, q are integers and q ≠ 0 are called rational numbers. Rational numbers are denoted by Q.
Even numbers: The numbers which are divisible by 2 successfully are called even numbers.
EX: 2, 4, 6, 8, 10, …
Odd numbers: The numbers which are not divisible by 2 are called Odd numbers.
Ex: 1, 3, 5,7, 9, 11, …
Note:
- The Sum of two even numbers is an even number.
- The Sum of two odd numbers is an odd number.
- The Sum of even and odd numbers is an odd number.
- The difference between the two even numbers is an even number.
- The difference between two odd numbers is an even number.
- The difference between even and odd numbers is an odd number.
- The product of two even numbers is an even number.
- The product of two odd numbers is an odd number.
- The product of even and odd numbers is an even number.
Prime numbers: The numbers, which have only two factors 1, and themselves are called prime numbers.
2, 3, 5, 7, …. Are prime numbers
Composite numbers: The number, which has more than two factors are called composite numbers.
4, 6,8,9…. are composite numbers.
Note – 1) 1 is neither prime nor composite
2) 2 is the smallest prime number
3) 4 is the smallest composite number.
Co – prime number: The number which has no common factor except 1 is called a co-prime number.
Ex: – (2, 3), (4,5) ……
Twin – primes: If the difference between two prime numbers is 2, then those numbers are called twin prime numbers.
Ex: – (2,3), (3,5), (17,19) ….
Special products:
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b) (a – b) = a2 − b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3 = a3 + b3 + 3ab (a + b)
(a – b)3 = a3 – 3a2b + 3ab2 – b3 = a3 – b3 – 3ab (a – b)
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
a3 + b3 = (a + b) (a2 – ab + b2)
a3 – b3 = (a – b) (a2 + ab + b2)
if a + b + c = 0, then a3 + b3 + c3 = 3abc.
Divisibility Rules
The process of checking whether a number is divisible by a given number or not without actual division is called the divisibility rule for that number.
Divisibility by 2: A number is divisible by 2 if its once place is either 0, 2, 4, 6, or 8.
Ex: 26 is divisible by 2. 35 not divisible by 2.
Divisibility by 3: If the sum of the digits of a number is divisible by 3, then that number is divisible by 3.
Ex: 231 → 2 + 3 +1 =6, 6 is divisible by 3
∴ 231 is divisible by 3
436 → 4 + 3 + 6 = 13, 13 is not divisible by 3
∴ 436 is not divisible by 3.
Divisibility by 4: If the last two digits of a number are divisible by 4, then that number is divisible by 4.
Ex: 436, 36 is divisible by 4 ∴ 436 is divisible by 4
623, 23 is not divisible by 4 ∴ 623 is not divisible by 4.
Divisibility by 5: A number is divisible by 5 if it’s one place is either 0 or 5.
Ex: 20, 25 are divisible by 5. 22, 46 are not divisible by 5.
Divisibility by 6: A number is divisible by 6 if it is divisible by both 3 and 2.
Ex: 242 is divisible by both 2 and 3 ∴ 242 is divisible by 6
232 is divisible by 3 but not 2 ∴ 232 is not divisible by 6
Divisibility rule by 7: –
First, multiply the last digit of a given number by 2,
subtract this result from the number formed by the remaining digits of a given number.
If that result is divisible by 7, then the given number is divisible by 7.
Ex: 112
Last digit is 2 ⇒ 2 × 2 = 4
Now 11 – 4 = 7
7 is divisible by 7
∴ 112 is divisible by 7.
Divisibility by 8: if the last three digits of a number are divisible by 8, then that number is divisible by 8.
Ex: 4232, last three digits 232 are divisible by 8
∴ 4232 is divisible by 8.
Divisibility by 9: if the sum of the digits of a number is divisible by 9, then that number is divisible by 9.
Ex: 459, 4 + 5 + 9 = 18 → 18 is divisible by 9 ∴ 459 is divisible by 9
532, 5 + 3 + 2 = 10 → 10 is not divisible by 9 ∴ 532 is not divisible by 9.
Divisibility by 10: – a number is divisible by 10 if its once place is 0.
Ex: 20 is divisible by 10. 22, 45 are not divisible by 10.
Factorial of a number: For positive integer ‘n’, the continued production of first natural numbers is called factorial n and is denoted by n!
Ex: 4! = 4 × 3 × 2 × 1 = 24
7! = 7 × 6 × 5× 4 × 3 × 2 × 1 = 5040
Absolute value or Modulus of a number: Absolute value of a number always gives a positive number.
Greatest integral value: The greatest integral value of a number ‘n’ is denoted by [n]
n <[n]< n + 1
Ex: [3.2] = 3; [5.6] = 5; [– 5. 4] = – 6
HCF and LCM
Factors: a number that divides the other number exactly is called a factor of that number.
6 = 1×6
= 2×3 ⟹ factors of 6 are: 1, 2, 3 and 6
Common factors: Common factors are those numbers, which are factors of all the given numbers.
Ex: 12, 9
Factors of 12 are: 1, 2, 3, 4, 6 and 12
Factors of 9 are: 1, 3 and 9
∴ Common factors of 12, 9 are 1,3
Perfect number: If the sum of the factors of a number (except the number itself) is equal to that number, then it is called a Perfect number.
Ex: 6
The factors of 6 are: 1, 2, 3, 6
1 + 2 + 3 = 6
Therefore 6 is a perfect number.
Highest Common Factor (H.C.F):- The highest common factor of two or more numbers is the highest of their common factors. It is also called ad Greatest Common Divisor (G.C.D).
Ex: H.C.F of 12, 9
Factors of 12 = 1, 2, 3,4, 6, 12
Factors of 9 = 1, 3, 9
Common factors of 12, 9 = 1,3
The highest common factor is 3
∴ H.C.F of 12, 9 is 3
Method of finding HCF:
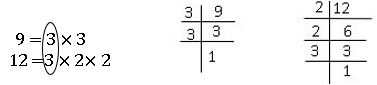
Prime factorization method: The HCF of 9, 12 can be found by the prime factorization method as follows.
Ex: – HCF of 9, 12
The common factor of 12, 9 is 3
∴ H.C.F of 12, 9 is 3
Continue division method: Euclid invented this method. Divide the larger number by smaller and then divide the previous divisor by the remainder until the remainder zero. The last divisor is the HCF of given numbers.
∴ HCF of 9, 12 is 3
Common multiple: multiples of 3 are 3, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39,42…
Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52….
Common multiples of 3 and 4 are 12, 24, 36….
Least common multiple (LCM): The least common multiple of two or more given numbers is the lowest of their common multiple.
Ex: LCM of 3 and 4
Multiples of 3 = 3, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39,42…
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52….
Common multiples of 3 and 4 = 12, 24, 36….
∴ LCM of 3, 4 is 12.
Methods of finding LCM:
Prime factorization method: –
The LCM of 6, 15 by using the prime factorization method is as follows:
Prime factors of 6 = 2 × 3
Prime factors of 15 = 5× 3
1.Express each number as a product of prime factors
2.Take the common factors both: 3
3.Take the extra factors of both 6 and 15 i.e., 2 and 5
4.The product of all common factors of two numbers and extra common factors of both finds LCM.
∴ LCM of 6 and 15 = (3) × 2 × 5 = 30.
Division method: – To find LCM of 6 and 15:
Arrange the given numbers in a row.
Then divide the least prime number, which divides at least two of the given numbers, and carry forward the numbers, which are not divisible by that number if any.
Repeat the process till no numbers have a common factor other than 1.
LCM is the product of the divisors and the remaining numbers.
Ex: – Find the LCM of 6, 15
∴ LCM of 6, 15 = 3 × 2 × 5 = 30.
Note: the product of LCM and HCF of given numbers = the product of given numbers.
Ex: – 6 × 15 = 30 × 3 = 90.
∎ HCF of co-prime numbers is 1 and LCM is their product
Fractions
Fraction: Fraction is a part of the whole. The whole may be a single object or group of objects.
In, 3 is the numerator and 4 is the denominator.
Proper fraction: if the numerator of a fraction is less than the denominator, then the fraction is called a proper fraction.
Improper fraction: if the numerator of a fraction is greater than the denominator, then the fraction is called an improper fraction.
Mixed fraction: An improper fraction can be written as a combination of a whole and part. Such a fraction is called a mixed fraction.
Decimal fractions: If the denominators of fractions are the powers of 10, then those fractions are called decimal fractions. We can write a decimal fraction with a decimal point (.). it makes it easier to do addition, subtraction, and multiplication on fractions.
Parts in a decimal fraction:
In a decimal fraction, a dot(.) or a decimal point separates the whole part of the number from the fractional part.
The part right side of the decimal point is called the decimal part of the number as it represents a part of 1. The part left to the decimal point is called the integral part of the number.
In 2.35, 2 is an integral part and 35 is the decimal part
It is read as two-point three five
Addition and Subtracting of Decimal Fractions:
while adding or subtracting decimal numbers, the digits in the same places must be added or subtracted.
While writing the numbers one below the other, the decimal points must become one below the other. Decimal places are made equal by placing zeroes on the right side of the decimal numbers.
Ex: Add 2.63, 4.1, 7.625
Subtract 3.12 from 5.327
Comparison of decimal numbers:
while comparing decimal numbers, first we compare the integral parts. If the integral parts are the same, then compare the decimal part.
Ex: – which is bigger: 13.5 or 14.5
Ans: 14.5
Which is bigger: 13.53 or 13. 25
Ans: 13.53
Multiplication of decimal fractions:
For example, we multiply 0.1 × 0.1
Multiplication of decimal fractions by 10, 100, and 1000: –
Here, we notice that the decimal point in the product shifts to the right side by as many zeroes as in 10, 100, and 1000.
Division of decimal fractions:
Division of decimal number by 10,100 and 1000:
Here, we notice that the decimal point in the product shifts to the left side by as many zeroes as in 10, 100, and 1000.
BODMAS Rule
B ⟶ Bracket
O ⟶ Off (Product)
D ⟶ Division
A ⟶ Addition
S ⟶ Subtraction
Ex: Solve: 7 – 12 ÷ 3 of 12
Sol: 7 – 12 ÷ 3 of 12 = 72 – 12 ÷ 3 of 2 ( 3 of 2 = 3× 2 = 6)
= 72 – 12 ÷ 6
= 72 – 2
= 70
Squares and Square roots, Cubes and Cube roots
Square: Square number is the number raised to power 2. The number obtained by the number multiplied by itself.
Ex: – 1) square of 5 = 52 = 5 × 5 = 25, 2) square of 3 = 32 = 3× 3 = 9
Perfect Square: A natural number is called a perfect square if it is the square of some natural number.
Ex: 1,4,9, …etc.
Square Root: the square root of a number x is that number when multiplied by itself gives x as the product. The square root of x is denoted by![]()
The square root of a number in decimal form
Make the no. of decimal places even, by affixing a zero, if necessary. Now periods and find out the square root by the long division method.
Put the decimal point in the square root as soon as the integral part is exhausted.
Ex: – To find the square root of 79.21
The square root of a decimal number which is not perfect square:
if the square root is required to correct up to two places of decimal, we shall find it up to 3 places of decimal and then round it off up to two decimal places.
if the square root is required to correct up to three places of decimal, we shall find it up to 4 places of decimal and then round it off up to three decimal places.
Ex: – To find the square root of 0.8 up to 2 decimal places
Pythagorean triplet:
Three natural numbers a, b and c are said to form a Pythagorean triplet if, c2 = a2 + b2
For every natural number a > 1, (2a, a2 – 1, a2 + 1).
Ex: – if we put a = 3 in (2a, a2 – 1, a2 + 1), then we get Pythagorean triplet (6, 8, 10).
Cube of a number:
The cube of a number is that number raised to the power 3.
Ex: – cube of 0.3 = 0.33 = 0.027
Cube of 2 = 23 = 8
Perfect cube:
If a number is a perfect cube, then it can be written as the cube of some natural numbers.
Ex: – 1, 8, 27 and so on.
Cube root:
The cube root of a number x is that number which when multiplied by itself three times gives x as the product.
Surds
If ‘a’ is a positive rational number that can be expressed as the nth power of some rational number, then the irrational number is called a Surd
![]() n is called the order of surd, a is called ‘radicand’
n is called the order of surd, a is called ‘radicand’
Mixed surd: A surd which has a rational factor other than 1, the other factor being irrational is called mixed surd.
Pure surd: A surd which unity has its rational factor, other factor being a rational factor is called Pure surd.
Rationalizing Factor (R.F): If the product of two surds is a rational number, then each of the two surds is a rationalizing factor of the other. It is not unique.
Laws of Radicals (Surds):
Logarithms
For any two positive integers a and x if aN = x then ![]()
Laws of logarithms:
Ratio
The comparison of two quantities of the same kind by using division is called ‘Ratio’
The ratio of two quantities ‘a’ and ‘b’ is denoted by a: b, read as a is to b
In a ratio a: b, a is called first term or antecedent and b is called second term or consequent.
Compound Ratio: The compound ratio of a: b and c : d is denoted by a: b:: c : d
a : b : : c : d = a × c : b × d
the compound ratio of ( a : b), (c : d) and( x : y) is acx : bdy
The duplicate ratio of a: b is a2: b2
Sub Duplicate ratio of a: b is ![]()
Triplicate ratio of a: b is a3: b3
Sub Triplicate ratio of a: b is ![]()
Allegation or Mixture
Allegation: Alligation is a rule, to find the ratio in which two or more quantities at the given price must be mixed to produce a mixture of the desired price.
Mixture: Mixture means mixing two or more quantities. It can be expressed in the form of percentage or ratio.
Mean price: The cost price of a unity quantity of the mixture is called the mean price.
Allegation Rule: If two quantities are mixed, then
Suppose a container contains ‘x’ units of liquid from which units are taken out and replaced by water. After n operations the quantity of pure liquid = ![]() units.
units.
Proportion
If two ratios are equal, then they are in proportion.
If a: b = c : d, then a, b, c and d are in proportion
a and d are extremes
b and c are means
product of means = product of extremes
Componendo and Dividendo: If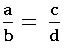 , then
, then 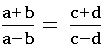
Unitary method: The method in which we first find the value of one unit and then the value of the required no. of units is known as the unitary method.
Direct proportion: In two quantities, when one quantity increase(decreases) the other quantity also increases(decreases) then two quantities are in direct proportion.
Inverse proportion: In two quantities, when one quantity increase(decreases) the other quantity also decreases (increases) then two quantities are in direct proportion.
Percentage
Per cent means per 100, ‘x’ per cent means ‘x’ hundredth.
Converting a fraction into a percentage:
Ex: Convert ![]() into the percentage
into the percentage
∎ If the price of commodity decreased by R%, then the increase in consumption so as not to
∎ If the price of commodity increased by R%, then the increase in consumption so as not to
Results on machines: If the present value of a machine is P and it deprecates at the rate of R% per year, then
Results on Population: If the present Population is P and it increases at the rate of R% per year, then
∎ If A is R% more than B, then B is less than A by ![]()
∎ If A is R% less than B, then B is more than A by![]()
Profit and loss
Cost price (C.P.): – Cost price is the price for which an article is bought or the price paid by a customer to buy an article.
Selling price (S.P.): – Selling price is the price for which an article is sold.
Profit: – If the Selling price is greater than the cost price, then we get the profit.
Profit = S.P – C.P.
Loss: – If the Selling price is less than the Cost price then, we get lost.
Loss = C.P – S.P.
Some formulae in profit and loss:
For-Profit:
For Loss:
∎ When a person sells two similar items, one at the gain of x%, and another one at a loss of x%, then the loss percentage
∎If the selling price is equal to cost price but uses false weight then
∎ if the selling price of an item is at a profit of x% but uses false weight which is y% less than the original weight then
∎ if the selling price of an item is at a loss of x% but uses false weight which is y% less than the original weight then
Simple interest
Principal: – The money which is borrowed is called ‘principal’(P).
Rate of interest: – percentage of interest per year is called the rate of interest(R).
Time: – The period for which money is called time(T).
Interest: – The money which is paid for the use of the principal is called interest (S.I).
Amount: – The total money which is paid after the expiry of the time is called the amount.
Amount = Principal + S.I
Compound Interest
Compound interest allows us to earn interest on interest.
Amount = 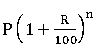 ( interest compounded annually)
( interest compounded annually)
P = principal, R = rate of interest, and n = no. of terms or time period.
Amount = 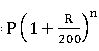 ( interest compounded half-yearly)
( interest compounded half-yearly)
∎When the rates are different for different years, like X%, Y%, and Z% for first, second and third year respectively, then
∎ the present worth of ₹ p due n years hence is given then present worth = 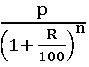
∎The time period after which interest is added to the principal is called the conversion period. When interest is compounded h yearly, there are two conversion periods in a year. In such a case, the half-year rate will be half of the annual rate.
Partnership
A business which is undertaken by two or more persons jointly is called ‘Partnership. Those persons are called Partners.
Types of Partnership:
The partnership is of two types (i) General or Simple partnership (ii) Compound partnership
(i) Simple partnership or General partnership:
In this type, the period of the investment is the same. Partners divide either profit and loss in the ratio of their investments.
If X and Y invests ₹x and ₹y respectively in a business for one year, then the end of the year
X’s share of profit: Share of s profit = x: y
(ii) Compound Partnership:
In this type, the investment and period of time are different. Their investments have to be reduced to invests per month or year. The profit or loss will be divided in the ratio of these converted investments.
If X invests ₹x perp months and Y invests ₹y per q months, then
X’s share of profit: Share of s profit = x: y
Time and work
∎ If A can do a piece of work in ‘x’ days, then A’s one day’s work =
∎ If A’s one-day work =1/x, then A can finish the work in ‘x’ days.
∎ If the work done by A is twice the work done by B, then
The ratio of work done by A and B is 2: 1
The ratio of time taken by A and B to finish the work is 1: 2
∎ If the work done by A is thrice as the work done by B, then
The ratio of work done by A and B is 3: 1
The ratio of time taken by A and B to finish the work is 1 : 3
Time and Distance
If the distance travelled = d, Speed = s and Time taken to travel = t, then
Distance = Speed × Time
⇒ d = s × t
∎ Relation between the speed in kilo metre per hour and speed in meter per seconds is
18 km/hr = 5 m/sec
Relative Speed:
∎ In the same direction relative speed = Difference of the Speeds
∎ In the opposite direction relative speed = sum of the Speeds
∎ If the two-object moving in the same direction with speeds x km/hr and y km/hr respectively, then their relative speed = (x – y) km/hr.
∎ If the two-object move in the opposite direction with speeds x km/hr and y km/hr respectively, then their relative speed = (x + y) km/hr.
∎ Time is taken to meet the object =![]()
Pipes and Cisterns
Inlet: A pipe connected with a tank or cistern, that fills it is called Inlet.
Outlet: A pipe connected with a tank or cistern, that emptying is called an outlet.
∎If a pipe can fill a tank in x hrs. then in one hour, it can fill l![]() part of the tank.
part of the tank.
∎If a pipe can empty a tank in y hrs. then in one hour, it can empty ![]() part of the tank.
part of the tank.
∎ If one pipe can fill a tank in x hrs. and another pipe can empty the full tank in y hrs. then on opening, both the pipes, the tank can fill in 1 hour = 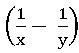
∎ If one pipe can fill a tank in x hrs. and another pipe can empty the full tank in y hrs. then on opening, both the pipes, the tank can empty in 1 hour =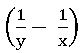
Boats and Streams
Downstream: In water, the direction along the water flow (stream) is called Downstream
Upstream: In water, the direction against the stream is called Upstream.
∎If the speed of an object moving in water is x km/hr and the speed of the water flow (stream) is y km/hr then
For upstream relative speed = (x – y) km/hr.
For downstream relative speed = (x + y) km/hr.
Speed in still water = ½ (x + y) km/hr
Rate of stream = ½ (x – y) km/hr
For Train Problems
∎ Time is taken by a train of length x meters to cross (pass) a pole (or a standing man) is equal to the time taken by the train to cover x meters.
∎ Time is taken by a train of length x meters to cross a stationary object (like a bridge) of lengthy meters is the time taken by train to cover (x + y) meters.
∎ If the two trains moving in the same direction with speeds x km/hr and y km/hr respectively, then their relative speed = (x – y) km/hr.
∎ If the two trains moving in the opposite direction with speeds x km/hr and y km/hr respectively, then their relative speed = (x + y) km/hr.
∎ If two trains of length meters and b meters are moving in opposite directions at x km/hr and y km/hr then the time taken by the trains to cross each other = ![]() hrs.
hrs.
∎ If two trains of length meters and b meters are moving in the same direction at x km/hr and y km/hr then the time taken by the trains to cross each other = ![]() hrs.
hrs.
Triangle
A closed figure with three-line segments is called a triangle.
A triangle has 3 sides, 3 angles, and 3 vertices.
Types of the triangle:
According to the sides:
Scalene triangle: – If no two sides of the triangle are equal then it is called a scalene triangle.
Isosceles triangle- If any two sides of a triangle are equal, then it is called an isosceles triangle.
Equilateral triangle: – If all sides of a triangle are equal, then it is called an equilateral triangle
According to the angles:
Acute angled triangle: – If all angles of a triangle are acute, then it is called an acute-angled triangle.
Right-angled triangle:– If one of the angles of a triangle is a right angle(900), then it is called a right-angled triangle.
Obtuse angled triangle: If one of the angles of a triangle is obtuse, then it is called an obtuse-angled triangle.
Relationship between the sides of a triangle:
∎In a triangle, the sum of the lengths of two sides is greater than the third side.
∎ In a triangle, the difference between the lengths of the two sides is less than the third side.
Altitude: In a triangle, a perpendicular line drawn from the vertex to its opposite side is called Altitude.
∎We can draw three altitudes in a triangle.
∎ In an Isosceles triangle, the altitude from the vertex bisects the base.
Median: In a triangle, a line drawn from the vertex to the midpoint of its opposite side is called the median.
∎We can draw three medians in a triangle.
∎ The median of a triangle divides it into two triangles of equal area.
Circumcentre:
The point of concurrency of medians in a triangle is called circumcentre.
∎ Circumcentre divides median in the ratio 2: 1.
Angle sum property of triangles:
Some of the angles in a triangle is 1800
An Exterior angle: The angle formed in the exterior of a triangle when one of the sides is produced is called an exterior of the triangle.
∎ An exterior angle of a triangle is equal to the sum of its interior opposite angles.
Vertical angle bisector theorem: The bisector of the vertical angle of a triangle divides the base in the ratio of the other two sides.
Similar triangles:
Two triangles are said to be similar if (i) their corresponding angles are equal (ii) their corresponding side are in proportion.
∎ The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
∎ The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding Altitudes.
Pythagorean theorem:
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In ∆ABC, ∠B = 900, then AC2 = AB2 + BC2
FORMULAE:
∎ Area of the triangle with base ‘b’ and height ‘h’ =![]() b × h sq. Units
b × h sq. Units
∎ Area of the triangle whose lengths of the sides a, b and c = ![]() sq. Units
sq. Units
∎ If a and b are the lengths of any two sides of a triangle and 𝛉 is the angle between them, then area of the triangle = ab sin 𝛉 sq. Units
∎ Area of an equilateral triangle with side a = ![]() a2 sq. Units
a2 sq. Units
∎The radius of the circumcircle of a triangle =![]()
∎ The radius of the circumcircle of an equilateral triangle of side a =![]()
∎ The radius of the incircle of a triangle of the area ∆ and semi perimeter s =![]()
∎ The radius of the incircle of an equilateral triangle of side a =![]()
Quadrilaterals
Quadrilateral: A simple closed figure with four-line segments is called a quadrilateral.
Diagonal: The line joining opposite vertices of a quadrilateral is called diagonal.
Trapezium: In a quadrilateral one pair of opposite sides are parallel, then it is called Trapezium.
∎ The line joining the midpoints of non-parallel sides of a trapezium is parallel to each of the parallel sides and equal to half of their sum.
Parallelogram: In a quadrilateral two pairs of opposite sides are parallel, then it is called Parallelogram.
∎ The diagonals of a parallelogram bisect each other and not equal.
∎ The diagonal of a parallelogram divides it into two triangles of equal area.
∎ In a parallelogram opposite sides are equal and opposite angles are equal.
Rectangle: In a parallelogram one of the angles is 900, then it is called a rectangle.
∎ In a rectangle, diagonal is bisect each other and equal.
Rhombus: In a parallel gram adjacent sides are equal, then it is called Rhombus.
∎ In a Rhombus diagonal are bisect each other perpendicularly and unequal.
A parallelogram and rectangle on the same base and lie between the same parallel lines are equal in area.
FORMULAE:
∎ Area of the Trapezium = ![]() (sum of the parallel sides) × (distance between them)
(sum of the parallel sides) × (distance between them)
∎ Area of the parallelogram = base × height
∎ Perimeter of rectangle = 2 (length + breadth)
Area if the rectangle = length × breadth
∎ Area of rhombus = ![]() × product of lengths of diagonals
× product of lengths of diagonals
∎ Perimeter of Square = 4 × side
Area of square = (side)2
∎Area of four walls of a room = 2 (length + breadth) × height
Circles:
Circle: A set of points that are at a constant distance from a fixed point is called a circle.
The fixed point is called the centre of the circle and the constant distance is called the radius of the circle.
∎ Circumference of the circle = 2πr, where r is the radius of the circle.
Area of the circle = πr2
∎Length of an Arc = l = rθ, where θ is the angle subtended by an arc at the centre.
∎Area of a regular polygon of side a = 1.72 a2
Quantitative Aptitude Mensuration
Cuboid:
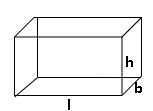
Lateral surface area (L.S.A) = 2h (l + b) square units.
Total surface area (T.S.A) = 2 (lb + bh + hl) square units.
Volume = lbh cubic units.
Cube:
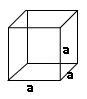
Lateral surface area (L.S.A) = 4 a2 square units.
Total surface area (T.S.A) = 6 a2 square units.
Volume = a3 cubic units.
Cylinder:
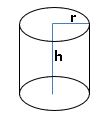
Curved surface area (C.S.A) = 2πr h square units.
Total surface area (T.S.A) = 2πr (r +h) square units.
Volume = πr2 h cubic units.
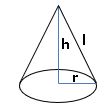
Cone:
Curved surface area (C.S.A) = πrl square units.
Total surface area (T.S.A) = πr (r +l) square units.
Volume = (R2 + r2 + Rr) πh cubic units.
Frustum of a cone:
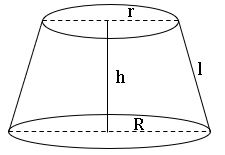
When a cone is cut by a plane parallel to the base of the cone then the portion between the plane and the base is called the frustum of the cone.
L.S.A = πl (r + R) square units.
T.S.A = πl [r2 + R2 + l (R + r)] square units.
Sphere:
Total surface area (T.S.A) = 4πr2 square units.
Hemisphere:
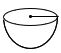
Curved surface area (C.S.A) = 2πr2 square units.
Total surface area (T.S.A) = 3πr2 square units.
Pyramid:
Surface area = Area of the base + Area of each of the lateral faces
Volume = ![]() × area of the base × height cubic units.
× area of the base × height cubic units.
Average:
∎ Average of n natural numbers = ½ (n + 1).
∎ suppose A person covers a certain distance at x km/hr and an equal distance at y km/hr, then the average speed during the whole journey is ![]() km/hr
km/hr
Probability:
Random Experiment: If in an experiment all the possible outcomes are known in advance and none of the outcomes can be predicted with certainty, then such an experiment is called a random experiment.
Ex: Throwing a die, Tossing A coin.
Events: The possible outcomes of a trial are called events.
To measure the chance of it happening numerically we classify them as follows:
Certain: Something that must happen
Equally likely: something that has the same chance of occurring.
Less likely: Something that would occur with less chance.
More likely: Something that would occur with more chance.
Impossible: Something that cannot happen.
Complimentary event: – Let E denote the event, ‘not E’ is called complimentary event of E. It is denoted by . P ( ) = 1 – P(E) ⟹ P ( ) +P(E) = 1.
∎0 ≤ P(E) ≤ 1
Deck of cards: – A deck of playing cards consists of 52 cards which are divided into 4 suits of 13 cards each. They are black spade, black clubs, red heart, and a red diamond. The cards in each suit are 2, 3, 4, 5, 6, 7, 8, 9,10, Ace, Jack, Queen, and King. Jack, Queen, and King are called face (picture) cards.
Calendar
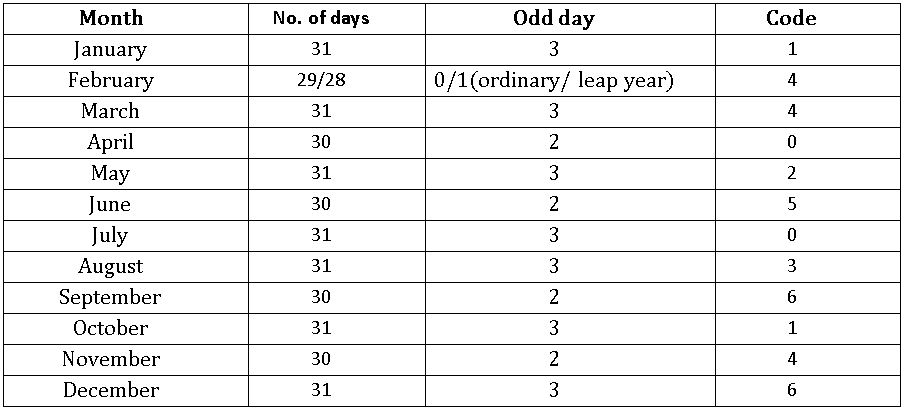
Ordinary year: A year having 365 days is called an ordinary year. In ordinary years we have 52 complete weeks and 1 extra day.
7 months ⟶ 31 days.
4 months ⟶ 30 days.
1 month (February) ⟶ 28 days.
Leap year: A year having 366 days is called a leap year. In leap years we have 52 complete weeks and 2 extra days.
7 months ⟶ 31 days.
4 months ⟶ 30 days.
1 month (February) ⟶ 29 days.
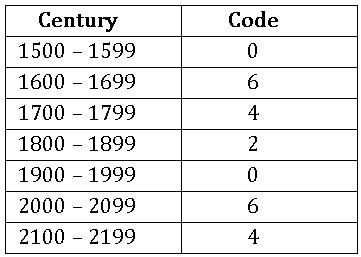
∎ A leap year is divisible by 4.
∎ A century to be a leap year if it must be divided by 400.
∎ In a century 76 ordinary years and 24 leap years.
Odd day: Extra days apart from the complete weeks in a given period is called an odd day.
∎ An ordinary year has 1 odd day.
∎ A leap year has two odd days.
∎ A century has 5 odd days. (76 × 1 + 24 × 2 = 124 odd days = 17 weeks = 5 odd days).
∎In 200 years ⟶ 3 odd days.
In 300 years ⟶ 1 odd day.
In 400 years ⟶ 0 odd day.
In 800 years ⟶ 0 odd day.
In 1200 years ⟶ 0 odd day.
Century − Code:
Month − odd day − Code:
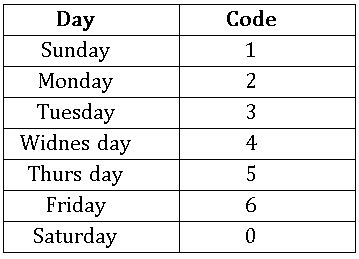
Day – Code:
Quantitative Aptitude Clocks
A clock has two hands (i) Shorter hand or hour hand (ii) Longer hand or Minute hand
∎For every hour, both hands coincide once.
Hour hand:
Angle made by Hour hand in 12 hours = 3600
In one hour, an hour hand can make the angle = 300.
In one minute, the hour hand can make the angle =![]()
Minute hand:
Angle made by Minute hand in 60 minutes = 3600
In one minute, Minute hand can make the angle = 60
Relative speed:
The relative speed of the Minute hand and Hour hand = 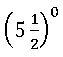 =
= 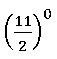
∎ When two hands are rotated in the clockwise direction
- They may be opposite to each other.
- They may coincide with each other.
- They may be perpendicular to each other.
Two hands – Coincide:
The angle between two hands = 00
In the span of 1 hour, they coincide only 1 time.
12 hours, they coincide 11 times.
1 day, they coincide 22 times.
Two hands – opposite direction:
The angle between two hands =1800
In the span of 1 hour, they coincide only 1 time.
12 hours, they coincide 11 times.
1 day, they coincide 22 times.
Two hands – perpendicular:
The angle between two hands = 900
In the span of 1 hour, they coincide 2 times.
12 hours, they coincide 22 times.
1 day, they coincide 44 times.
∎ When two hands are opposite to each other than those two hands are 30 minutes spaces apart.
∎ When two hands are perpendicular to each other than those two hands are 15 minutes spaces apart.
Formula:
Where M = Minutes
H = Hours (starting hour)
θ = angle between two hands
If starting hour is at 12’O clock, then take H = 0
Quantitative Aptitude
Visit My Youtube Channel: Click on the Logo