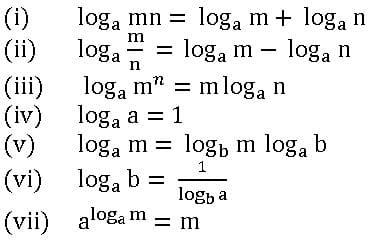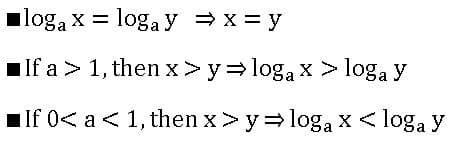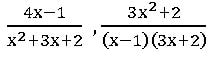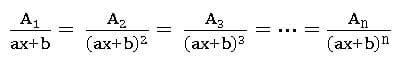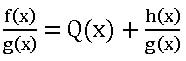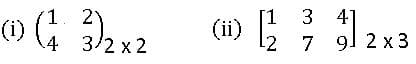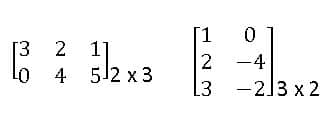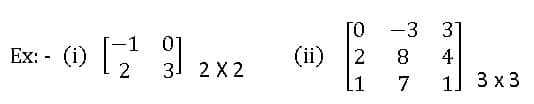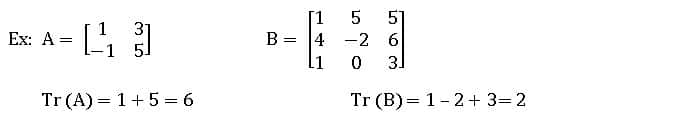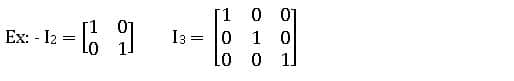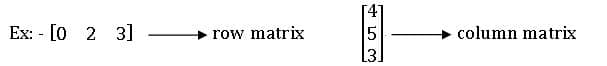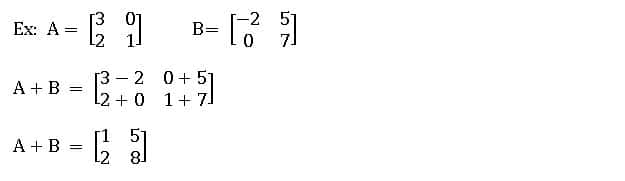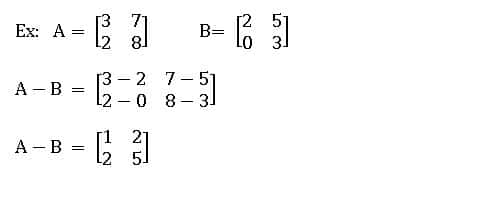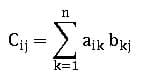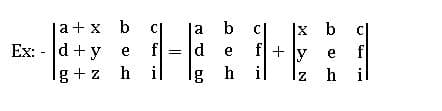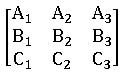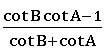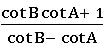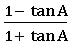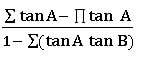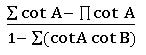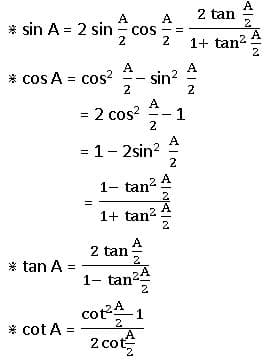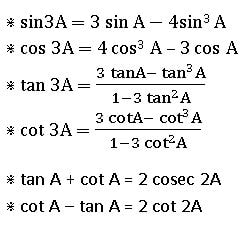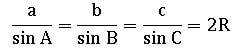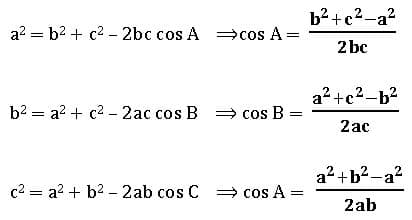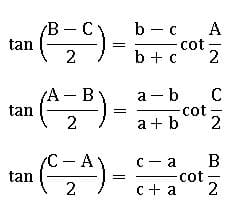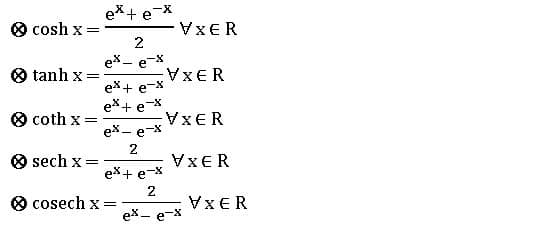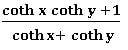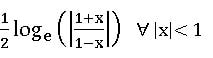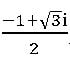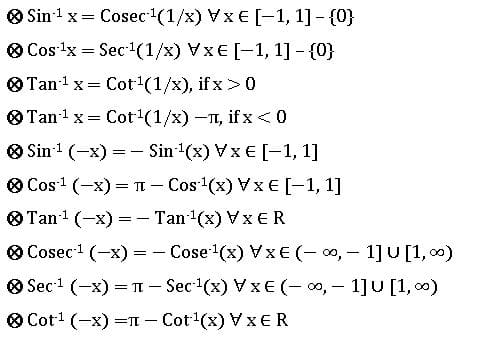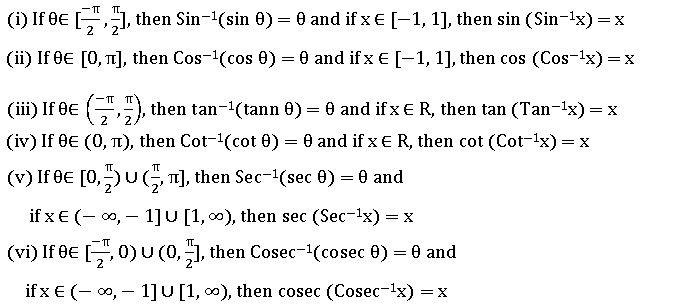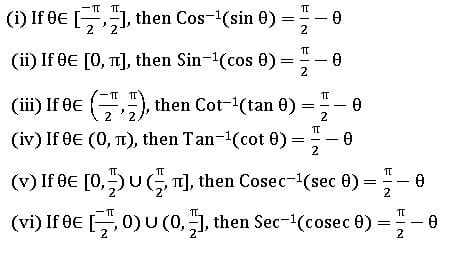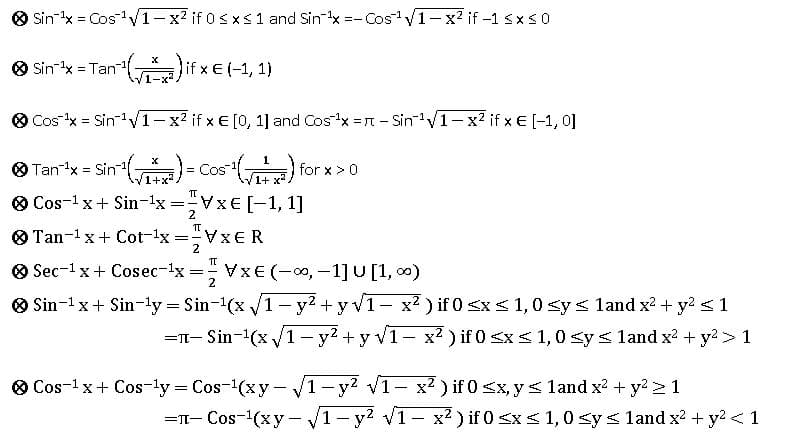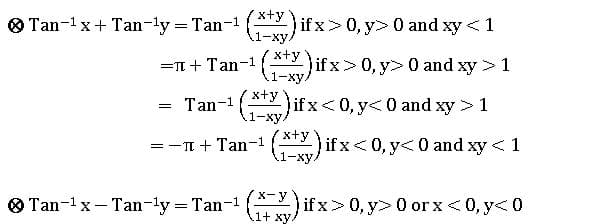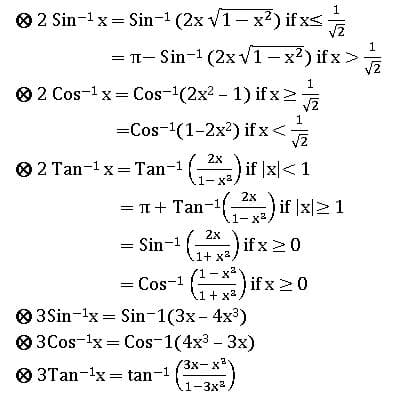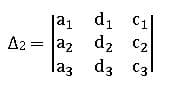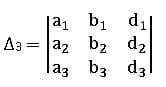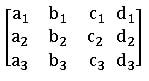Engineering Mathematics SEM – 1Concept

Polytechnic Sem 1 – Engineering Mathematics

Polytechnic Sem 1 –  Notes for Polytechnic SEM – 1 is Designed by the ” Basics in Maths” team. Here we can learn Concepts in Basic Engineering mathematics at Polytechnic Sem – I.

 This Material is very Useful for Basic Engineering Mathematics Polytechnic Sem – I Students.

By learning These Notes, Basic Engineering Mathematics Polytechnic Sem – I Students can Write their Exam successfully and fearlessly.

 LOGARITHMS

Logarithm: For ant two positive real numbers a, b, and a ≠ 1. If the real number x such then a^x = b, then x is called logarithm of b to the base a. it is denoted by

Standard formulae of logarithms:

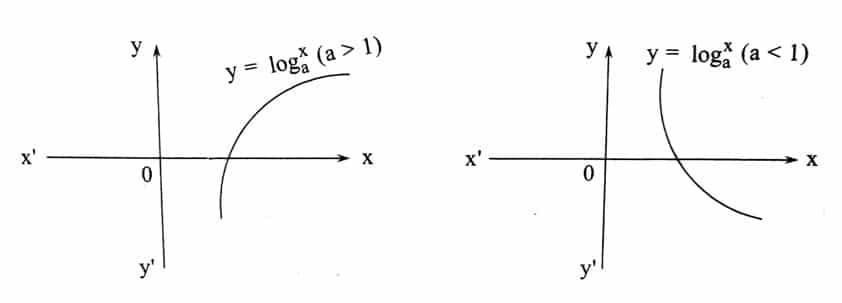
Logarithmic Function:

Let a be a positive real number and a ≠ 1. The function f: (o, ∞) → R Defined by f(x) =

PARTIAL FRACTIONS

Fractions:

If f(x) and g(x) are two polynomials, g(x) ≠ 0, then   is called rational fraction.

Ex:

   etc.  are rational fractions.

Proper Fraction:

A rational fraction is said to be a Proper fraction if the degree of g(x) is greater than the degree of f(x).

Ex:

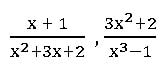  etc. are the proper fractions.

Improper Fraction:

A rational fraction is said to be an Improper fraction if the degree of g(x) is less than the degree of f(x).

Ex:

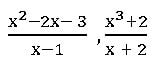 etc. are the Improper fractions.

Partial Fractions:

Expressing rational fractions as the sum of two or more simpler fractions is called resolving a given fraction into a partial fraction.

∎ If R(x) =  is proper fraction, then

Case(i): – For every factor of g(x) of the form (ax + b) ⁿ, there will be a sum of n partial fractions of the form:

Case(ii): – For every factor of g(x) of the form (ax² + bx + c) ⁿ, there will be a sum of n partial fractions of the form:

∎ If R(x) = is improper fraction, then

Case (i): – If degree f(x) = degree of g(x),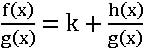   where k is the quotient of the highest degree term of f(x) and g(x).

Case (ii): – If f(x) > g(x)

R(x) =

 MATRICES AND DETERMINANTS

Matrix: A set of numbers arranged in the form of a rectangular array having rows and columns is called Matrix.

•Matrices are generally enclosed by brackets like

•Matrices are denoted by capital letters A, B, C, and so on

•Elements in a matrix are real or complex numbers; real or complex real-valued functions.

Oder of Matrix: A matrix having ‘m’ rows and ‘n’ columns is said to be of order m x n read as m by n.

Ex:

Types Of Matrices

Rectangular Matrix: A matrix in which the no. of rows is not equal to the no. of columns is called a rectangular matrix.                 

 Square Matrix: A matrix in which the no. of rows is equal to no. of columns is called a square matrix.

Principal diagonal (diagonal) Matrix: If A = [a _ij] is a square matrix of order ‘n’ the elements a₁₁, a₂₂, a₃₃, ………. A_{n n} is said to constitute its principal diagonal.

Trace Matrix: The sum of the elements of the principal diagonal of a square matrix A is called the trace of the matrix. It is denoted by Tr (A).

Diagonal Matrix: If each non-diagonal element of a square matrix is ‘zero’ then the matrix is called a diagonal matrix.

Scalar Matrix: If each non-diagonal element of a square matrix is ‘zero’ and all diagonal elements are equal to each other, then it is called a scalar matrix.

Identity Matrix or Unit Matrix: If each of the non-diagonal elements of a square matrix is ‘zero’ and all diagonal elements are equal to ‘1’, then that matrix is called unit matrix

Null Matrix or Zero Matrix: If each element of a matrix is zero, then it is called a null matrix.

Row matrix & column Matrix: A matrix with only one row s called a row matrix and a matrix with only one column is called a column matrix.

Triangular matrices:

A square matrix A = [a_ij] is said to be upper triangular if a_ij = 0   ∀ i > j

A square matrix A = [a_ij] is said to be lower triangular matrix a_ij = 0  ∀ i < j

Equality of matrices:

matrices A and B are said to be equal if A and B are of the same order and the corresponding elements of A and B are equal.

Addition of matrices:

If A and B are two matrices of the same order, then the matrix obtained by adding the corresponding elements of A and B is called the sum of A and B. It is denoted by A + B.

Subtraction of matrices:

If A and B are two matrices of the same order, then the matrix obtained by subtracting the corresponding elements of A and B is called the difference from A to B.

Product of Matrices:

Let A = [a_ik]_mxn and B = [b_kj]_nxp be two matrices, then the matrix C = [c_ij]_mxp   where

Note: Matrix multiplication of two matrices is possible when no. of columns of the first matrix is equal to no. of rows of the second matrix.

A _{m x n}  . B_{p x q} = AB _{mx q}; n = p

Transpose of Matrix: If A = [a_ij] is an m x n matrix, then the matrix obtained by interchanging the rows and columns is called the transpose of A. It is denoted by A^I or A^T.

Note: (i) (A^I)^I = A     (ii) (k A^I) = k . A^I    (iii)  (A + B )^T = A^T + B^T  (iv)  (AB)^T = B^TA^T

Symmetric Matrix: A square matrix A is said to be symmetric if A^T =A

If A is a symmetric matrix, then A + A^T is symmetric.

Skew-Symmetric Matrix: A square matrix A is said to be skew-symmetric if A^T = -A

If A is a skew-symmetric matrix, then A – A^T is skew-symmetric.

 Minor of an element: Consider a square matrix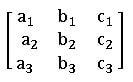

the minor element in this matrix is defined as the determinant of the 2×2 matrix obtained after deleting the rows and the columns in which the element is present.

Ex: – minor of a₃ is     = b₁c₂ – b₂c₁

Minor of b₂ is   = a₁c₃ – a₃c₁

Cofactor of an element: The cofactor of an element in i ^th row and j ^th column of A_3×3 matrix is defined as its minor multiplied by (- 1) ^i+j.

Properties of determinants:

If each element of a row (column) f a square matrix is zero, then the determinant of that matrix is zero.

Ex: –    A =   ⇒ det(A) = 0

If A is a square matrix of order 3 and k is scalar then.

If two rows (columns) of a square matrix are identical (same), then Det. Of that matrix is zero.

Ex: –    A =     ⇒ det(A) = 0

If each element in a row (column) of a square matrix is the sum of two numbers then its determinant can be expressed as the sum of the determinants.

Ex: – 

If each element of a square matrix are polynomials in x and its determinant is zero when x = a, then (x-a) is a factor of that matrix.

For any square matrix A Det(A) = Det (A^I).

Det (AB) = Det(A). Det(B).

For any positive integer n Det (Aⁿ) = (DetA)ⁿ.

Singular and non-singular matrices:

A Square matrix is said to be singular if its determinant is is zero, otherwise it is said to be non-singular matrix.

Ex: –   A =      det(A) = 4 – 4 = 0

∴ A is singular matrix

B =

Det(B) = 4 + 4 = 8≠ 0

∴ B is non-singular

 Adjoint of a matrix: The transpose of the matrix formed by replacing the elements of a square matrix A with the corresponding cofactors is called the adjoint of A.

Let A = and     cofactor matrix of A =

Then adj (A) =

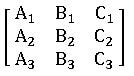
 Invertible matrix: Let A be a square matrix, we say that A is invertible if there exists a matrix B such that AB =BA = I, where I is a unit matrix of the same order as A and B.

1. (A^{– I})^{– I} = A
2. (A^I)^{– I} = (A^-I)^I
3. (AB)^-I = B^-I A^-I
4. A^-I =

Compound Angles

The algebraic sum of two or more angles is called a ‘compound angle’. Thus, angles A + B, A – B, A + B + C etc., are Compound Angles

For any two real numbers A and B

⋇ sin (A + B) = sin A cos B + cos A Cos B

⋇ sin (A − B) = sin A cos B − cos A Cos B

⋇ cos (A + B) = cos A cos B − sin A sin B

⋇ cos (A − B) = cos A cos B + sin A sin B

⋇ tan (A + B) =

⋇ tan (A − B) =

⋇ cot (A + B) =

⋇ cot (A − B) =

⋇ tan ( + A) =

⋇ tan ( − A) =

⋇ cot (+ A) =

⋇ cot (− A) =

⋇ sin (A + B + C) = ∑sin A cos B cos C − sin A sin B sin C  

⋇ cos (A + B + C) = cos A cos B cos C− ∑cos A sin B sin C 

⋇ tan (A + B + C) =

⋇ cot (A + B + C) =

⋇ sin (A + B) sin (A – B) = sin² A – sin² B = cos² B – cos² A

⋇ cos (A + B) cos (A – B) = cos² A – sin² B = cos² B – sin² A

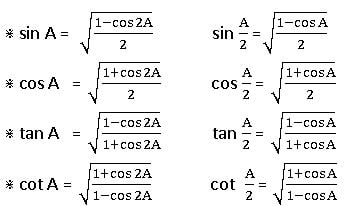
Multiple and Sub Multiple Angles

If A is an angle, then its integral multiples 2A, 3A, 4A, … are called ‘multiple angles ‘of A and the multiple of A by fraction like are called ‘submultiple angles.

∎ If  is not an add multiple of

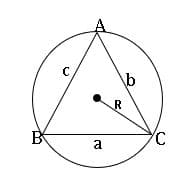
PROPERTIES OF TRIANGLES

In ∆ABC,

Lengths AB = c; BC = a; AC =b

The area of the triangle is denoted by ∆.

Perimeter of the triangle = 2s = a + b + c

A = ∠CAB; B = ∠ABC; C = ∠BCA.

R is circumradius.

Sine rule:

In ∆ABC,

⟹ a = 2R sin A; b = 2R sin B; c = 2R sin C

Where R is the circumradius and a, b, c, are lengths of the sides of ∆ABC.

Cosine rule:

In ∆ABC,

Projection rule:

In ∆ABC,

a = b cos C + c cos B

b = a cos C + c cos A

c = a cos B + b cos A

Tangent rule (Napier’s analogy):

 Area of the triangle:

In ∆ABC, a, b, and c are sides

S = and area of the triangle

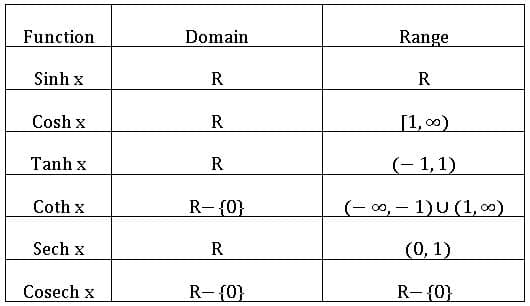
HYPERBOLIC FUNCTIONS

⨂

⨂ The function f: R→R defined by f(x) =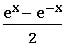 ∀ x ∈ R is called the ‘hyperbolic sin’ function. It is denoted by Sinh x.

∴Sinh x =

Similarly,

Identities:

⨂ cosh²x – sinh² x = 1

cosh²x = 1 + sinh² x

sinh² x = cosh² x – 1

⨂ sech² x = 1 – tanh² x

tanh² x = 1 – sesh² x

⨂ cosech² x = coth² x – 1

coth² x = 1 + coth² x

Addition formulas of hyperbolic functions:

⨂ Sinh (x + y) = Sinh x Cosh y + Cosh x Sinh y

⨂ Sinh (x − y) = Sinh x Cosh y − Cosh x Sinh y

⨂ Cosh (x + y) = Cosh x Cosh y + Sinh x Sinh y  

⨂ Cosh (x − y) = Cosh x Cosh y − Sinh x Sinh y 

⨂ tanh (x + y) =

⨂ tanh (x − y) =

⨂ coth (x + y) =

⨂ sinh 2x = 2 sinh x cosh 2x =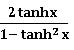

⨂ cosh 2x = cosh²x + sinh² x = 2 cosh²x – 1 = 1 + 2 sinh²x =

⨂ tanh 2x =

Inverse hyperbolic functions:

⨂ Sinh⁻¹x =  ∀ x ∈ R

⨂ Cosh⁻¹x =   ∀ x ∈ (1, ∞)

⨂ Tanh⁻¹x =    ∀ < 1

COMPLEX NUMBERS

The equation x² + 1 = 0 has no roots in real number system.

∴ scientists imagined a number ‘i’ such that i² = − 1.

Complex number:

if x, y are any two real numbers then the general form of the complex number is

z = x + i y; where x real part and y is the imaginary part.

3 + 4i, 2 – 5i, – 3 + 2i are the examples for Complex numbers.

• z = x +i y can be written as (x, y).
• If z₁ = x₁ + i y₁, z₂ = x₂ + i y₂, then
• z_{1 +} z₂ = (x₁ + x₂, y₁ + y₂) = (x₁ + x₂) + i (y₁ + y₂)
• z_{1 −} z₂ = (x₁ − x₂, y₁ − y₂) = (x₁ − x₂) + i (y₁ − y₂)
• z_1∙   z₂ = (x₁ x₂ −y₁ y₂, x₁y₂ + x₂y₁) = (x₁x₂ −y₁ y₂) + i (x₁y₂ +x₂ y₁)
• z_1/ z_{2 = (}x₁x₂ + y₁ y₂/x₂² +y₂², x₂ y₁ – x₁y₂/ x₂² +y₂²)

= (x₁x₂ + y₁ y₂/x₂² +y₂²) + i (x₂ y₁ – x₁y₂/ x₂² +y₂²)

  Multiplicative inverse of complex number:

   The multiplicative inverse of the complex number z is 1/z.

z = x + i y then 1/z = x – i y/ x² + y²

Conjugate complex numbers:

The complex numbers x + i y, x – i y are called conjugate complex numbers.

Conjugate of z is denoted by

The sum and product of two conjugate complex numbers are real.

If z₁, z₂ are two complex numbers then

 Modulus and amplitude of complex numbers:

Modulus: – If z = x + i y, then the non-negative real number is called modulus of z and it is denoted by or ‘r’.

Amplitude: – The complex number z = x + i y represented by the point P (x, y) on the XOY plane. ∠XOP = θ is called amplitude of z or argument of z.

x = r cos θ, y = r sin θ

x² + y² = r² cos²θ + r² sin²θ = r² (cos²θ + sin²θ) = r²(1)

⇒ x² + y² = r²

⇒ r =  and = r.

• Arg (z) = tan⁻¹(y/x)

• Arg (z₁.z₂) = Arg (z₁) + Arg (z₂) + nπ for some n ∈ { −1, 0, 1}

• Arg(z₁/z₂) = Arg (z₁) − Arg (z₂) + nπ for some n ∈ { −1, 0, 1}

Note:

∎ e^iθ = cos θ + i sin θ

∎ e^−iθ = cos θ − i sin θ

De-Moiver’s theorem

For any integer n and real number θ, (cos θ + i sin θ) ⁿ = cos n θ + i sin n θ.

→ cos α + i sin α can be written as cis α

→ cis α.cis β= cis (α + β)

→ 1/cisα = cis(-α)

→ cisα/cisβ = cis (α – β)

⟹ (cos θ + i sin θ) ^-n = cos n θ – i sin n θ

⟹ (cos θ + i sin θ) (cos θ – i sin θ) = cos²θ – i² sin²θ = cos²θ + sin²θ = 1.

→ cos θ + i sin θ = 1/ cos θ – i sin θ and cos θ – i sin θ = 1/ cos θ + i sin θ

⟹ (cos θ – i sin θ) ⁿ = (1/ (cos θ –+i sin θ)) ⁿ = (cos θ + i sin θ)^-n = cos n θ – i sin n θ

n^th root of a complex number: let n be a positive integer and z₀ ≠ 0 be a given complex number. Any complex number z satisfying z ⁿ = z₀ is called an n^th root of z₀. It is denoted by z₀^1/n or

⟹ let z = r (cos θ + i sin θ) ≠ 0 and n be a positive integer. For k∈ {0, 1, 2, 3…, (n – 1)}

let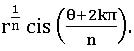 Then a₀, a₁, a_{2, …,} a_n-1 are all n distinct n^th roots of z and any n^th root of z is coincided with one of them.

n^th root of unity:  Let n be a positive integer greater than 1 and 

Note:

• The sum of the n^th roots of unity is zero.
• The product of n^th roots of unity is (– 1) ^{n – 1}.
• The n^th roots of unity 1, ω, ω², …, ω^n-1 are in geometric progression with common ratio ω.

Cube root of unity:      

x³ – 1 = 0 ⇒ x³ = 1

x =1^1/3

cube roots of unity are: 1    

ω =  , ω² =

ω² +ω + 1 = 0 and ω³ = 1

TRANSFORMATIONS

For A, B∈ R

⋇ sin (A + B) + sin (A – B) = 2sin A cos B

⋇ sin (A + B) −sin (A – B) = 2cos A sin B

⋇ cos (A + B) + cos (A – B) = 2 cos A cos B

⋇ cos (A + B) − cos (A – B) = − 2sin A sin B

For any two real numbers C and D

⋇ sin C + sin D = 2sin cos

⋇ sin C −sin D= 2cos  sin

⋇ cos C + cos D = 2 cos   cos

⋇ cos C − cos D = − 2sin   sin

If A + B + C = π or 180⁰, then

⋇ sin (A + B) = sin C; sin (B + C) = sin A; sin (A + C) = sin B

⋇ cos (A + B) = − cos C; cos (B + C) = −cos A; cos (A + C) = − cos B

If A + B + C = 90⁰ or then

⋇ sin   = cos;   sin   = cos ;  sin   = cos

⋇ cos  = sin; cos   = sin; cos   = sin

If    then

⋇ sin (A + B) = cos C; sin (B + C) = cos A; sin (A + C) = cos B

⋇ cos (A + B) = sin C; cos (B + C) = sin A; cos (A + C) = sin B

Polytechnic Sem 1

INVERSE TRIGONOMETRIC RATIOS

If A, B are two sets and f: A→ B is a bijection, then f^-1 is existing and f^-1: B → A is an inverse function.

Properties of Inverse Trigonometric functions:

Engineering Mathematics

Solutions of Simultaneous Equations

Matrix Inversion Method:

Let a system of simultaneous equations be

a₁ x + b₁ y + c₁z = d₁

a₂ x + b₂ y + c₂z = d₂

a₃ x + b₃ y + c₃z = d₃

The matrix form of the above equations is

Therefore, the matrix equation is AX = B

If Det A ≠ 0, A^-1 is exists

X = A^-1 B

By using above Condition, we get the values of x, y and z

This method is called as Matrix Inversion Method

Cramer’s Method:

Let a system of simultaneous equations be

a₁ x + b₁ y + c₁z = d₁

a₂ x + b₂ y + c₂z = d₂

a₃ x + b₃ y + c₃z = d₃

∆₁ is obtained by replacing the coefficients of x (1^st column elements of ∆) by constant values

∆₂ is obtained by replacing the coefficients of y (2^nd column elements of ∆) by constant values

∆₃ is obtained by replacing the coefficients of z (3^rd column elements of ∆) by constant values

Now

This method is called Cramer’s Method

Gauss-Jordan Method:

Let a system of simultaneous equations be

a₁ x + b₁ y + c₁z = d₁

a₂ x + b₂ y + c₂z = d₂

a₃ x + b₃ y + c₃z = d₃

Augmented matrix: The coefficient matrix (A) augmented with the constant column matrix (B) is called the augmented matrix. It is denoted by [AD].

[AD] =

This Matrix is reduced to the standard form ofby using row operations

1. Interchanging any two rows
2. Multiplying the elements of any two elements by a constant.
3. Adding to the elements of one row with the corresponding elements of another row multiplied by a constant.

∴ The solution of a given system of simultaneous equations is x = α, y = β, and z = γ.

Procedure to get the standard form:

1. Take the coefficient of x as the unity as a first equation.
2. If 1 is there in the first-row first column, then make the remaining two elements in the first column zero.
3. After that, if one element in R₂ or R₃ is 1, then make the remaining two elements in that column C₂ or C₃ as zeroes.
4. If any row contains two elements as zeros and only non-zero divide that row elements with the non-zero element to get unity and make the remaining two elements in that column as zeros.

Engineering Mathematics

PDF FILE: Mathematics Notes 4 Polytechnic SEM – I

Visit my Youtube Channel: Click on Below Logo