Complex Numbers 4 Marks IMP Q & A | TS Inter Maths 2A
Complex Numbers 4 Marks
Are you preparing for the TS Inter Maths 2A exam and worried about the 4-mark questions on complex numbers? This page is designed exactly for you.
Here you will find important 4-mark questions with clear, step-by-step answers, based strictly on the Telangana Board exam pattern. Each question is explained thoroughly so that students can understand the logic, remember formulas easily, and write perfect answers in the exam.
This content is highly useful for last-minute revision, exam writing practice, and scoring full marks in Complex Numbers. Ideal for intermediate 2nd-year students, especially those who want clarity without confusion.
1. If x + iy = 
, then show that 4x2 – 1 = 0
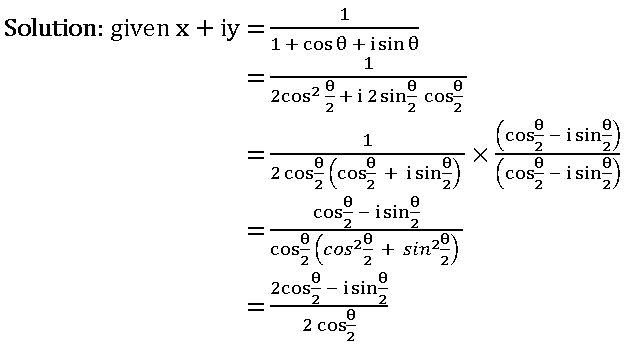
x + iy =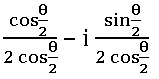 
x + iy = 
compare real parts on both sides
x = 1/2 ⟹ 2x = 1
Squaring on both sides
4x2 = 1 ⟹ 4x2 – 1 = 0
Hence proved
2. Show that the points in the Argand plane represented by the complex numbers
–2 + 7i, 
, 4 – 3i, 
(1 + i) are the vertices of a rhombus.
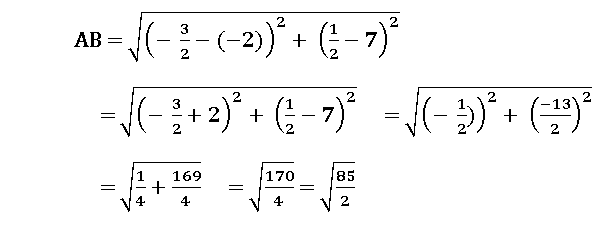
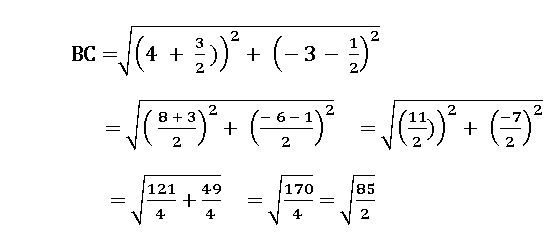
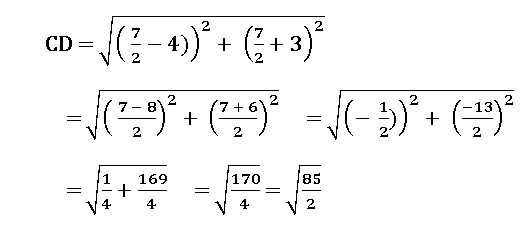
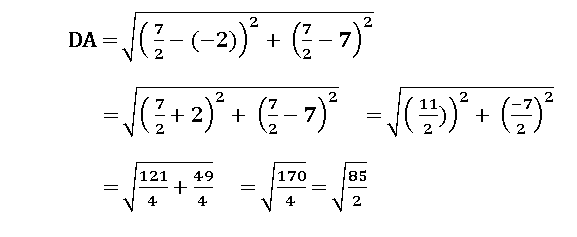
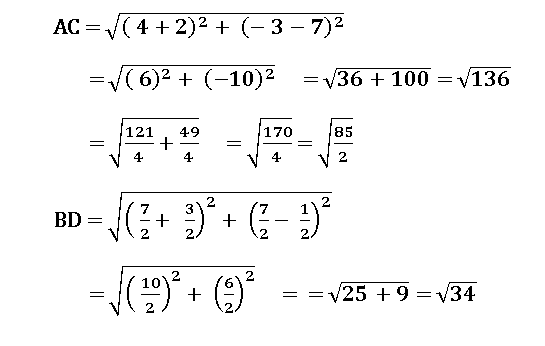
∴ AB = BC = CD = DA and AC ≠ BD
∴ The given points form a rhombus.
3. If z = x + iy, and if the point in the Argand plane represents z. Find the locus of z satisfying the equation |z – 3 + i| = 4
Solution: z = x + iy
|z – 3 + i| = 4
Substitute the z value in the above equation
⟹ |x + iy – 3 + i| = 4
⟹ |(x – 3) + i (y + 1)| = 4
We know that, the modulus of a complex number x + iy = 
⟹ 
= 4
⟹ (x – 3)2 + (y + 1)2 = 16
∴ The locus of z is (x – 3)2 + (y + 1)2 = 16
4.
