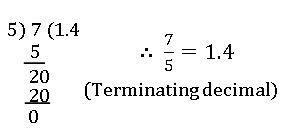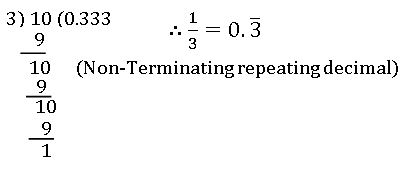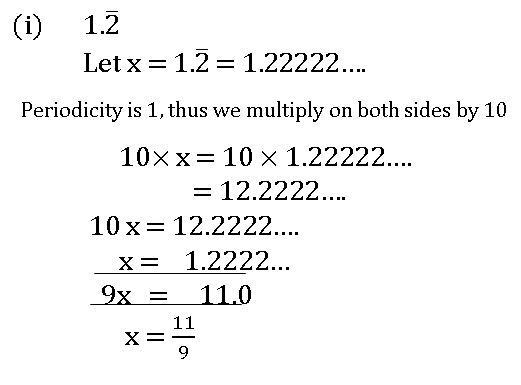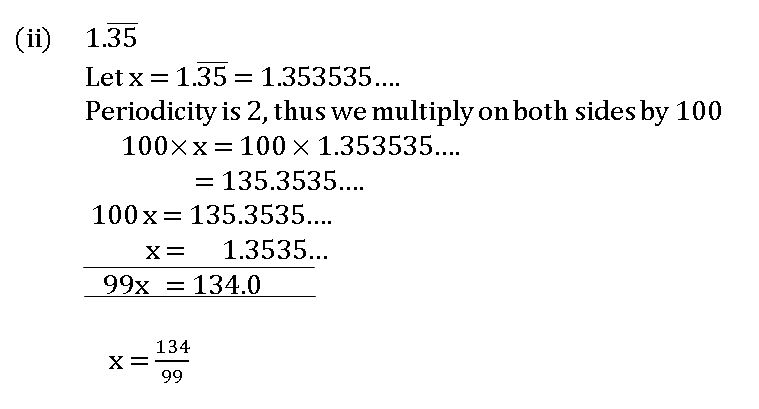ICSE Class 9 Maths Made Easy: From Confusion to Confidence

ICSE Class 9 Maths Made Easy

ICSE Class 9 Maths

9th Class Maths Concept: This note is prepared by the Basics in Maths team.These notes help ICSE 9th class Maths students develop interest in mathematics and remove fear.

These notes cover all the topics covered in the ICSE 9^thclass Maths syllabus and include plenty of formulae and concepts to help you solve all the types of ICSE 9^th

Math problems appear in CBSE board and entrance examinations

ICSE Class 9 Maths Made Easy

1. RATIONAL AND IRRATIONAL NUMBERS

Natural numbers: counting numbers 1, 2, 3… called Natural numbers.The symbol N represents natural numbers.

N = {1, 2, 3…}

Whole numbers: Natural numbers with 0 form whole numbers. The symbol W represents whole numbers.

W = {0, 1, 2, 3…}

Integers: Integers include zero, whole numbers greater than zero, and whole numbers less than zero. They are represented by I or Z.

Z = {…-3, -2, -1, 0, 1, 2, 3…}

Rational number

Any number expressed as p/q, with p and q as integers and q ≠ 0, is known as a rational number. The symbol used is Q.

∗ A rational number may have both its numerator and denominator positive or negative. For convenience, the denominator is assumed not to be negative.

Ex: $\inline \fn_jvn -\frac{2}{3}$ can be written as $\inline \fn_jvn \frac{-2}{3}=\frac{2}{-3}$

but our convenience, we can take $\inline \fn_jvn \frac{-2}{3}$

Equal rational numbers:

For any 4 integers a, b, c, and d (b, d ≠ 0), we have $\inline \fn_jvn \frac{a}{b}=\frac{c}{d}$ ⇒ ad = bc

The order of Rational numbers:

If are two rational numbers such that b> 0 and d > 0

then $\inline \fn_jvn \frac{a}{b}> \frac{c}{d}$ ⇒ ad > bc

Absolute value of rational numbers:

The absolute value of a rational number is always positive. The absolute value of $\inline \fn_jvn \frac{a}{b}$ is denoted by $\inline \fn_jvn \left | \frac{a}{b} \right |$ .

Ex: – absolute value of $\inline \fn_jvn -\frac{2}{3}=\frac{2}{3}$

To find a rational number between given numbers:

Mean method: – A rational number between two numbers a and b is $\inline \dpi{120} \fn_jvn \frac{a + b}{2}$

Ex: – insert two rational numbers between 1 and 2

1 < $\inline \dpi{120} \fn_jvn \frac{1 + 2}{2}$ < 2 ⟹ 1 < $\inline \dpi{120} \fn_jvn \frac{3}{2}$ < 2

1 < $\inline \dpi{120} \fn_jvn \frac{3}{2}$ $\inline \dpi{120} \fn_jvn < \frac{\frac{3}2{+2}}{2}$ < 2 ⟹ 1 < $\inline \dpi{120} \fn_jvn \frac{3}{2}< \frac{7}{4}$ $\dpi{120} \fn_jvn <$ 2

To rational numbers in a single step: –

Ex:- insert two rational numbers between 1 and 2

To find two rational numbers, we can use 1 and 2 as rational numbers with the same denominator, 3

(∵ 1 + 2 = 3)

1 = $\fn_jvn \frac{1\times 3}{3}$ and 2 = $\inline \dpi{120} \fn_jvn \frac{2\times 3}{3}$

$\inline \dpi{120} \fn_jvn \frac{3}{3}\left ( 1 \right )< \frac{4}{3}< \frac{5}{3}< \frac{6}{3}\left ( 2 \right )$

Note: – There are infinitely many rational numbers between two numbers.

The decimal form of rational numbers

∗ A rational number is written either as a terminating decimal or as a non-terminating repeating decimal.

Converting decimal form into $\dpi{120} \fn_jvn \frac{p}{q}$ the form:

1. Terminating decimals: –

1.2 = $\inline \dpi{120} \fn_jvn \frac{12}{10}=\frac{6}{5}$

1.35 = $\inline \dpi{120} \fn_jvn \frac{135}{100}=\frac{27}{20}$

2. Non-Terminating repeating decimals: –

Irrational numbers:

The numbers which are not written in the form of $\dpi{120} \fn_cm \frac{p}{q}$ , where p, q are integers, and q ≠ 0 are called rational numbers. Rational numbers are denoted by Q^Ior S.
Every irrational number is expressed as a non-terminating, non-repeating decimal.

Ex:- $\dpi{120} \fn_cm \sqrt{2},\, \sqrt{5},\pi$ and so on.

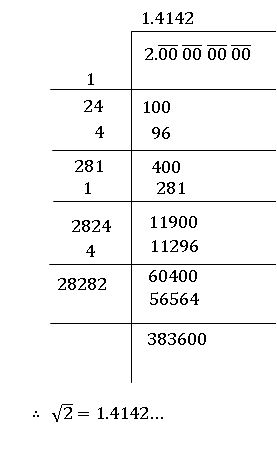
Calculation of square roots:
There is a reference to irrationals in the calculation of square roots in the Sulba Sutra.
Procedure for finding $\dpi{120} \fn_cm \sqrt{2}$ value: