TS polycet
For TS Polycet || Solved Previous Question Papers 2020 MathTs polycet|| Maths solved previous qp 2020 || Solved Papers
TS polycet solved previous qp 2020

The State Board of Technical Education and Training (SBTET), Telangana, Hyderabad, will conduct “Polytechnic Common Entrance Test (TS POLYCET)” for the candidates seeking admission into all Diploma Courses in Engineering /Non-Engineering Technology.
The Main Subjects in this
TS Polycet
Exams are Maths, Physics, Chemistry and Biology. Here we are providing the Previous Maths Papers Questions and Solutions.
The syllabus of Maths, Physics, Chemistry and Biology for TS POLYCET-2020 is the same as that of SSC Examination conducted by the Board of Secondary Education, Telangana.
TS Polycet || Solved Previous Question Papers 2021 Mathematics gives an idea becuase, it is very helpful to solve the problems in TS POLYCET entence examination
TS Polycet Solved Question Papers
TS Polycet
Ts polycet solved previous qp 2020
Chapter 1: Real Numbers
1.If 7 divides a2 then
a2 ను 7 భాగించినచో
(1) 7 divides a (a ను 7 భాగిస్తుంది)
(2) 7 divides ![]() (
( ![]() ను 7 భాగిస్తుంది)
ను 7 భాగిస్తుంది)
(3) a divide 7 (7 ను a భాగిస్తుంది)
(4) none (ఏదీ కాదు)
Answer: (1)
2. In the formula ![]() , which of the following is true?
, which of the following is true?
![]() అయిన, ఈ క్రింది వాటిలో ఏది సత్యము.
అయిన, ఈ క్రింది వాటిలో ఏది సత్యము.
(1) x > 0, y > 0, a = 1
(2) x < 0, y < 0, a = 1
(3) a > 0, y > 0, x = 1
(4) x > 0, y > 0, a ≠ 1
Answer: (4)
3. 5 =____________
Answer: (3)
4.![]() then x =
then x =
 అయిన, x =
అయిన, x =
(1) n (2) 1 (3) 5 (4) 2
Answer: (4)
5.  , ac = ___
, ac = ___
 అయిన, ac = ___
అయిన, ac = ___
(1)a2 (2)b2 (3) c2 (4) None(ఏది కాదు)
Answer: (2)
TS 10th class maths concept (E/M)
TS 10th Class Maths Concept (T/M)
TS Polycet

Chapter 2: Sets
1.Cardinal number of set A = {P, O, L, Y, T, E, C, H, N, I, Q} , B = {P, O, L, Y, C, E, T, 2020}, then B – A =
A = {P, O, L, Y, T, E, C, H, N, I, Q} , B = {P, O, L, Y, C, E, T, 2020}, అయిన B – A =
(1) {20} (2) {2020} (3) {40} (4) none (ఏది కాదు)
Answer: (2)
2. If A = {a} and B = {a, b} , C = {a, b, c}, then A ∩ B ∩ C =
A = {a} and B = {a, b} , C = {a, b, c}, అయిన A ∩ B ∩ C =
(1) {a} (2) {b}
(3) {c} (4) {2021}
Answer: (1)
TS 10th class maths concept (E/M)

Chapter 3: Polynomials
1. Product of the polynomials (x3 – 8), (x – 8) is denoted by p(x) = ax4 + bx3 + c x2 + dx +e, then p (8) =
(x3 – 8), (x – 8) అను బహుపదుల లబ్దము p(x) = ax4 + bx3 + c x2 + dx +e అయిన, p (8) =
(1) 0 (2) 1
(3) 2 (4) 3
Answer: (1)
2. If α, β are the zeroes of x2 – 1 , α + β =
α, β లు x2 – 1అనే వర్గ బహుపదికి శూన్యాలు అయితే α + β విలువ?
(1) 0 (2) 1
(3) – 1 (4) 2
Answer: (1)

Chapter 4: Linear equations in Two Variables
1.For the equation 2019x + 2020y = 4040, when x= 0 the value of y =
2019x + 2020y = 4040 అను సమీకరణమునకు x= 0 అయిన, y విలువ
(1) 2020 (2) 2019
(3) 4 (4) 2
Answer: (4)
2. Solution of the equations 7x + 5y = 12 and 5x – 7y = – 2, not equal to
7x + 5y = 12 మరియు 5x – 7y = – 2 సమీకరణాల సాధన ఈ క్రిది వానీలో దేనికి సమాన కాదు
Answer: (1)
3. If 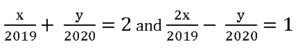 then (x, y) =
then (x, y) =
![]() అయిన,(x, y) =
అయిన,(x, y) =
(1) (2019, 2020) (2) (2020, 2019)
(3) (2019, 2019) (4) (2020, 2020)
Answer: (1)
4. If (5, 2) is the solution 2x + 3y = 20, ax – by = 0, the (a, b) =
2x + 3y = 20, ax – by = 0 ల సాధన (5, 2) అయిన (a, b) =
(1) (2, 5) (2) (5, 2)
(3) (– 2, 5) (4) (– 5, 2)
Answer: (1)
5. If the system of equations x – y = 1 and ax + y = 2 has unique solution then
జత సమీకరణాలకు x – y = 1, ax + y = 2 లకు ఏకైక సాధన ఉంటే
(1) a = 1 (2) a = – 1
(3) a ≠ 1 (4) a ≠– 1
Answer: (4)
6. x + y =  , x – y = 0, then x =
, x – y = 0, then x =
x + y = , x – y = 0, అయిన x =
, x – y = 0, అయిన x =
Answer: (3)
TS 10th class maths concept (E/M)

Chapter 5: Quadratic Equations
1.If the roots of 2x2 + kx + 3 = 0 are real and equal, then k =
2x2 + kx + 3 = 0 యొక్క మూలాలు వాస్తవాలు మరియు సమానాలు అయిన k విలువ =
(1)± 6 ![]() (2) ± 4
(2) ± 4
(2)± 2 ![]() (4) ± 5
(4) ± 5
Answer: (3)
2. 8x2 – 6x – 9 = 0= ______
(1)(2x – 3) (x – 3) (2) (2x – 3) (x +1)
(3) (2x + 1) (x – 1) (4) (2x – 3) (4x + 3)
Answer: (4)
4. Roots of 5x2 – 8x = 4 are
5x2 – 8x = 4 యొక్క మూలాలు
(1) 2, ![]() (2) 1,
(2) 1,![]()
(3) 2, ![]() (4) 2, 7
(4) 2, 7
Answer: (1)
TS Polycet
TS 10th class maths concept (E/M)

Chapter 6: Progressions
1. 1, -1/2, 1/4…. Are in G.P, then find 8th term
1, -1/2, 1/4…. అనే గుణ శ్రేడిలోని ఎనిమిదవ పదం
(1) 1/128 (2) 1/64
(3) – 1/128 (4) –1/64
Answer: (3)
2. 4, 7, 10… are in AP, the sum 15 terms is____
4, 7, 10… A.P లో ఉన్నచో 15 పదాల మొత్తం ____
(1) 385 (2) 475
(3) 375 (4) 325
Answer: (3)
3. 10th term of AP: 13, 8, 3, – 2, …. is
13, 8, 3, – 2, …. అను అంకశ్రేడిలోని 10 వ పదం
(1) – 32 (2) – 23
(3) 30 (4) – 30
Answer: (1)
4. Which term of GP:  is 729?
is 729?
![]() అనే గుణ శ్రేడిలో 729 ఎన్నవ పదం?
అనే గుణ శ్రేడిలో 729 ఎన్నవ పదం?
(1) 10 (2) 12 (3) 14 (4) 16
Answer: (2)

Chapter 7: Coordinater Geometry
1.If the slope of the line through (2, – 7) and (x, 5) is 3 then x =_________
(2, – 7), (x, 5) ల గుండా పోవు రేఖ వాలు 3 అయిన x యొక్క విలువ _____
(1) 4 (2) 5 (3) 6 (4) 7
Answer: (3)
2. If (8, 1), (k, – 4), (2, – 5) are collinear, then k = ______
(8, 1), (k, – 4), (2, – 5) లు సరేఖీయాలైన k యొక్క విలువ ______
(1) 4 (2) 3 (3) 2 (4) 1
Answer: (2)
3. The point (2, – 3) divides the line segment joining the points (– 1, 3), (4, – 7) in the ratio__
(– 1, 3), (4, – 7) బిందువులతో ఏర్పడు రేఖా ఖండాన్ని (2, – 3) బిందువు విభజించు నిష్పత్తి___
(1) 3: 2 (2) 2 : 3 (3) 8 : 1 (4) 1 : 4
Answer: (1)
4. The centroid of the triangle whose vertices are (3, – 5), (–7, 4), (10, –2) is
(3, – 5), (–7, 4), (10, –2) లు శీర్శాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రం____
(1) (1, 1) (2) (1, – 2) (3) (–2, 1) (4) (2, –1)
Answer: (4)

Chapter 8: Similar Triangles
1. If ∆ ABC ~ ∆ PQR; ∠A = 320, ∠R = 650, then ∠B =
If ∆ ABC ~ ∆ PQR; ∠A = 320, ∠R = 650, అయిన ∠B =
(1) 930 (2) 830 (3) 730 (4) 630
Answer: (2)
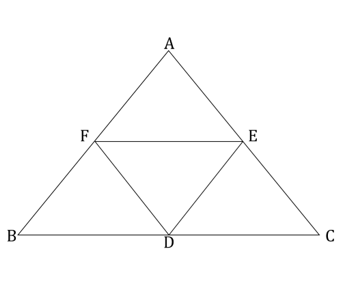
2. In the ∆ ABC; D, E and F are midpoints of the side BC, CA and AB.T
hen area of ∆ DEF : ∆ ABC = __________
∆ ABC లో D, E మరియు F లు వరుసగా BC, CA మరియు AB ల మధ్య బిన్డువులైన,
∆ DEF వైశాల్యం : ∆ ABC వైశాల్యం = __________
(1) 1 : 4 (2) 4 : 1 (3) 1 : 3 (4) 3 : 4
Answer: (1)
TS Polycet
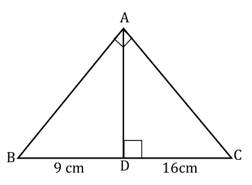
3. In the given figure ∠BAC = 900, AD ⊥ BC, BD = 9 cm and CD = 16 cm then AC =?
ఇచ్చిన పటం నుండి ∠BAC = 900, AD ⊥ BC , BD = 9 cm మరియు CD = 16 cm అయిన AC = ?
(1) 10 cm (2) 15 cm (3) 20 cm (4) 25 cm
Answer: (3)
4. The base of two similar triangles are 24 cm and 18 cm. If one side of first triangle is 8 cm,
then the corresponding side of another triangle is _______
రెండు సరూప త్రిభుజాల పొడవులు 24 cm మరియు 18 cm. ఒక త్రిభుజ భుజం 8 cm అయిన, రెండవ
అనురూప త్రిభుజ భుజం
(1) 8 cm (2) 6 cm (3) 4 cm (4) 2 cm
Answer: (2)
Chapter 9: Tangents and Secants to a Circle
1. The angle in a minor segment is ______ angle
అల్పవ్రుత్త ఖండం లోని కోణం _______ కోణం
(1) obtuse (అధిక) (2) acute (అల్ప) (3) right (లంబ) (4) straight (సరళ)
Answer: (1)
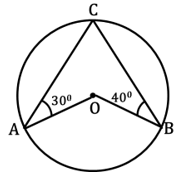
2. In the figure ∠CAO = 300, ∠CBO = 400, then ∠AOB =?
పటం నుండి ∠CAO = 300, ∠CBO = 400అయిన, ∠AOB =?
(1) 1000 (2) 1200 (3) 1400 (4) 1500
Answer: (3)
3. In the figure OB = 13 cm, OP ⊥ AB, OP = 12 cm then AB =_______
పటం నుండి OB = 13 cm, OP ⊥ AB, OP = 12 cm అయిన AB =_______
(1) 100 cm (2) 50 cm (3) 75 cm (4) 10 cm
Answer: (4)
4. If a parallelogram is cyclic, then it is a _________
సమాంతర చతుర్భుజం చక్రీయమైన, అది ఒక _________
(1) Rectangle (దీర్ఘ చతురస్రం) (2) Square (చతురస్రం)
(3) Quadrilateral (చతుర్భుజం) (4) Rhombus (రాంబస్)
Answer: (1)
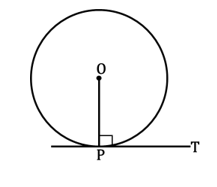
5. The angle at tangent to a circle and radius drawn at the point of contact is
స్పర్శ బిందువు వద్ద వృత్త స్పర్శ రేఖతో దాని వ్యాసార్థం చేయు కోణం
(1) 600 (2) 900 (3) 450 (4) 300
Answer: (2)
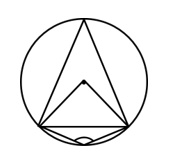
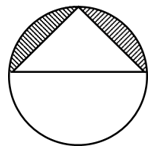
6. In the figure, AP = 12 cm, PB = 16cm. Let π = 3, then the perimeter of shaded portion is
పటం నుండి AP = 12 cm, PB = 16cm. π = 3 అయిన, షేడ్ చేసిన ప్రాంతం యొక్క చుట్టుకొలత ఎంత?
(1) 52 cm (2) 58 cm (3) 56 cm (4) 62 cm
Answer: (2)
TS Polycet
Chapter 10: Mensuration
1. If the perimeter of a rhombus is 52 cm, if one of the diagonals is 24 cm then the length of the
other diagonal is
ఒక రాంబస్ యొక్క చుట్టుకొలత 52 సెం.మీ. మరియు దాని ఒక కర్ణం 24 సెం.మీ. అయిన దాని రెండవ
కర్ణం పొడవు ఎంత ?
(1)5 cm (2)7 cm (3) 9 cm (4) 10 cm
Answer: (4)
2. The Radius of a cone is 7m and its height is 10 m. Then its slant height is _______
ఒక శంఖువు యొక్క వ్యాసార్టం 7మీ. మరియు నిలువు ఎత్తు 10 మీ. అయిన ఏటవాలు ఎత్తు_______
(1) 2 m (2) 13.5 m (3) 14.5 m (4) 16.2 m
Answer: (1)
3. The ratio of volumes of two cones is 4 : 5 and the ratio of radii of their bases is 2 : 3, then the
ratio of their vertical height is
రెండు శంఖువుల ఘనపరిమాణం ల నిష్పత్తి 4 : 5 మరియు వాటి వ్యాసార్తాల నిష్పత్తి 2 : 3 అయిన,
వాటి నిలువు ఎత్తుల నిష్పత్తి
(1) 4 : 5 (2) 9 : 5 (3) 3 : 5 (4) 2 : 5
Answer: (1)
4. Three cubes of sides 6cm, 8 cm and 1 cm are melted to form a new cube then the length of the
edge of the new cube is
6cm, 8 cm మరియు 1 cm భుజాలుగా గల సమ ఘనాలను కరిగించి ఒక పెద్ద ఘనం తయారు
చేయగా ఆ ఘనం యొక్క భుజం కొలత ఎంత?
(1) 9 cm (2) 8 cm (3) 7 cm (4) 6 cm
Answer: (1)
5. If the diameter of a sphere is ‘d’ then its volume is
ఒక గోళం యొక్క వ్యాసం ‘d’ అయిన , దాని ఘనపరిమాణం
![]()
Answer: (1)
Solution:
6. A reservoir in the shape of a frustum of a right circular cone. It is 8 m across at the top and
4m cross at the bottom. It is 6m deep then its capacity is
ఒక రిజర్వాయర్ షటేల్ కాక్ పైబాగం ఫ్రస్టం ఆకారం లో గలదు. దాని పైన మరియు క్రింది వ్యాసాలు 8
మీ., 4 మీ. మరియు లోతు 6 మీ.అయిన, దాని ఘనపరిమాణం ఎంత?
(1) 174 m3 (2) 176 m3 (3) 127 m3 (4) 170 m3
Answer: (2)
TS Polycet
Chapter 11: Trigonometry
1. If a cos θ + b sin θ = p; a sin θ – b cos θ = q then
a cos θ + b sin θ = p; a sin θ – b cos θ = q అయిన
(1) a2 + b2 = p2 + q2 (2) a2 + b2 = p2 – q2 (3) a2 – b2 = p2 + q2 (4) a2 – b2 = p2 – q2
Answer: (1)
2. 1 radian =
(1) 56018’ (2) 57016’ (3) 56015’ (4) 45040’
Answer: (2)
3. If A = 450, B = 600 then sin A + cos B =
A = 450 మరియు B = 600 అయిన sin A + cos B = ?
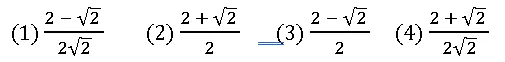
Answer: (2)
4. If A, B, C, D are angles of a cyclic quadrilateral, then sin A + sin B – sin C – sin D =?
A, B, C, D ఒక చక్రీయ చతుర్భుజ కోణాలైన sin A + sin B – sin C – sin D = ?
(1) – 1 (2) 0 (3) 1 (4) 2
Answer: (2)
5. If A = π/4, then (1 + tan A) (1 + tan2A) (1 + tan3A) =
A = π/4 అయితే (1 + tan A) (1 + tan2A) (1 + tan3A) =
(1) 6 (2) 4 (3) 8 (4) 2
Answer: (3)
6. cos 2010 cos 2020 cos 2030 …… cos 3000 =
cos 2010 cos 2020 cos 2030 …… cos 3000 విలువ ఎంత?
![]()
Answer: (3)
Chapter 12: Application of Trigonometry
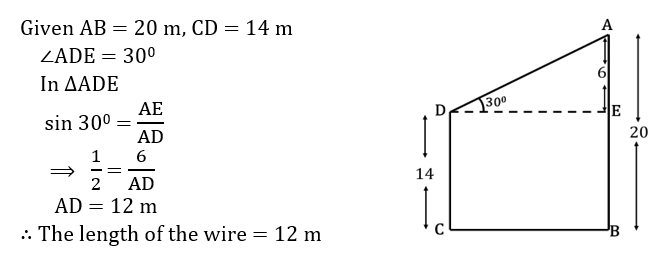
1. The tops of two poles are of height 20 m and 14 m are connected by a wire. If the wire makes an angle 300 with the horizontal, then the length of the wire is
20 మీ. మరియు 14 మీ. పొడవులు గల రెండు స్తంభాల కోనల్నితాడుతో కలిపారు. ఆ తాడు క్షితిజ సమాంతర రేఖతో 300 కోణం చేసిన, ఆ తాడు యొక్క పొడవు
(1) 11m (2) 12 m (3) 13 m (4) 10 m
Answer: (2)
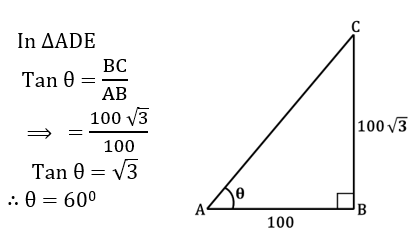
2. From the figure, θ = __________
పటం నుండి θ = __________
(1) 450 (2) 600 (3) 300 (4) 750
Answer: (2)
TS Polycet
Chapter 13: Probability
1. P(x) + P (“not x”) =
P(x) + P (“x కానిది”) =
(1) – 1 (2) – 2 (3) 1 (4) 2
Answer: (3)
2. If a two-digit number is choosen at random, then the probability that number choosen is a multiple of 3.
రెండంకెల సంఖ్యలో ఒక డాన్ని తీసుకుంటే, అది 3 యొక్క గుణిజమయ్యే సంభావ్యత

Answer: (2)
3. A die is thrown twice, then the probability of 5 will come up at least once.
ఒక పాచికను రెండు సార్లు దోర్లిస్తే కనీసం ఒకసారి ముఖంపై 5 వచ్చు సంభావ్యత

Answer: (1)
4. Three coins are tossed simultaneously, then the probability of getting at least two heads is
మూడు నాణాలను వరుసగా ఎగుర వేస్తే, కనీసం రెండు బారుసలు వచ్చే సంభావ్యత

Chapter 14: Statistics
1. If the mean of 6, 7, x, 8, y, 14 is 9 then x + y =_____________
6, 7, x, 8, y, 14 ల సగటు 9 అయిన, x + y =_____________
(1) 17 (2) 18 (3) 19 (4) 20
Answer: (3)
2. The A.M of 30 students is 42. Among them, two students get zero marks, then A.M of the remaining students is
30 మంది విద్యార్థుల సగటు 42. వారిలో ఇద్దరికి ‘0’ మార్కులు వస్తే మిగిలిన విద్యార్తుల సగటు
(1) 40 (2) 45 (3) 50 (4) 55
Answer: (2)
3. The median of 17, 31, 12, 27, 15, 19, 23 is
17, 31, 12, 27, 15, 19, 23 ల యొక్క మధ్యగతం
(1) 19 (2) 20 (3) 21 (4) 22
Answer: (1)
4. Mode of A, B, C, D, …., Z is
A, B, C, D, …., Z ల యొక్క బాహులకం
(1) 20 (2) 21 (3) 22 (4) no mode (బాహులకం ఉండదు)
Answer: (4)


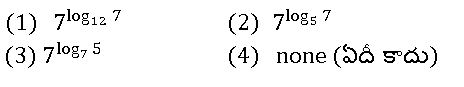
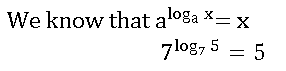
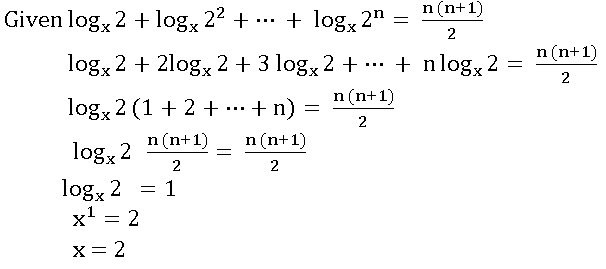
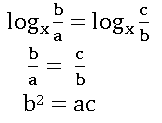
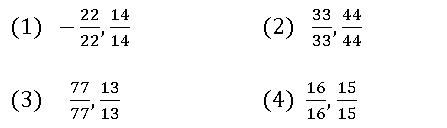
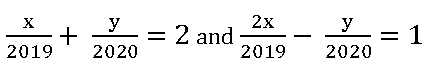

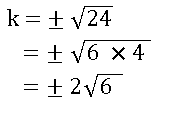

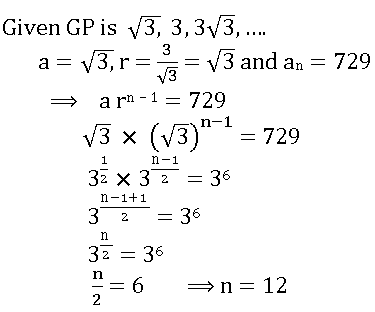

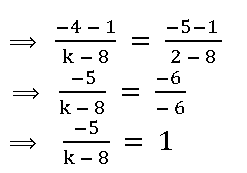
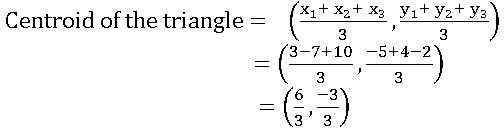

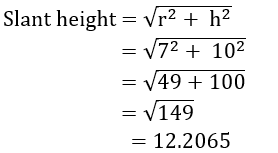
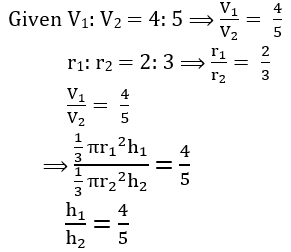
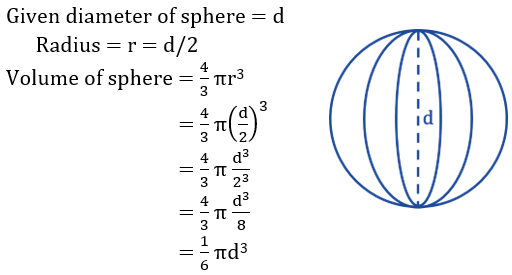
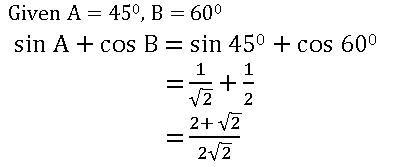
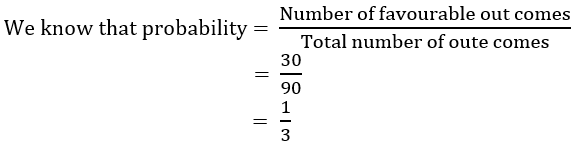

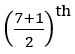 observation
observation
